Baixe Mechanics of Materials: Stress and Strain Analysis e outras Exercícios em PDF para Mecânica, somente na Docsity!
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
P1.1 A steel bar of rectangular cross section, 15 mm by 60 mm, is loaded by a compressive force of
110 kN that acts in the longitudinal direction of the bar. Compute the average normal stress in the bar.
Solution
The cross-sectional area of the steel bar is
( )( )
2 A = 15 mm 60 mm =900 mm
The normal stress in the bar is
( )( ) 2
110 kN 1,000 N/kN 122.222 MPa 900 m
m
2.2 MPa
F
A
σ = = = = Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
P1.2 A circular pipe with outside diameter of 4.5 in. and wall thickness of 0.375 in. is subjected to an
axial tensile force of 42,000 lb. Compute the average normal stress in the pipe.
Solution
The outside diameter D , the inside diameter d , and the wall thickness t are related by
D = d + 2 t
Therefore, the inside diameter of the pipe is
d = D − 2 t = 4.5 in. − 2 0.375 in. ( ) =3.75 in.
The cross-sectional area of the pipe is
2 2 2 2 2 4.5 in. 3.75 in. 4.8597 in. 4 4
A D d
π π = − = ^ − =
The average normal stress in the pipe is
2
42,000 lb 8,642.6 psi 4.8597 in.
8,640 psi
F
A
σ = = = = Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
P1.4 Three solid bars, each with square cross sections, make up the axial assembly shown in Figure
P1.4/5. Two loads of P = 30 kN are applied to the assembly at flange B , two loads of Q = 18 kN are
applied at C , and one load of R = 42 kN is applied at end D. The bar dimensions are b 1 = 60 mm, b 2 =
20 mm, and b 3 = 40 mm. Determine the normal stress in each bar.
FIGURE P1.4/
Solution
Cut an FBD through bar (1). The FBD should include the free end of the assembly at D. We will
assume that the internal force in bar (1) is tension. From equilibrium, the force in bar (1) is
( ) ( )
1
1
2 2 2 30 kN 2 18 kN 42 kN 66 kN 66 kN (C)
F x F P Q R
F P Q R
From the given width of bar (1), the cross-sectional area of bar (1) is
( )
2 2 2 A 1 (^) = b 1 = 60 mm =3,600 mm
and thus, the normal stress in bar (1) is
1 (^ )(^ ) (^1 ) 1
66 kN 1,000 N/kN 18.333 MPa 3,
mm
33 MPa (C)
F
A
σ
= = = − = Ans.
Cut an FBD through bar (2). The FBD should include the free end of the assembly at D. We will
assume that the internal force in bar (2) is tension. From equilibrium, the force in bar (2) is
( )
2
2
2 2 18 kN 42 kN 6 kN 6 kN (C)
F x F Q R
F Q R
From the given width of bar (2), the cross-sectional area of bar (2) is
( )
2 2 2 A 2 (^) = b 2 = 20 mm =400 mm
The normal stress in bar (2) is
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
2 (^ )(^ ) (^2 ) 2
6 kN 1,000 N/kN 15.000 MPa 400 mm
15.00 MPa (C)
F
A
σ
= = = − = Ans.
Cut an FBD through bar (3). The FBD should include the free end of the assembly at D. We will
assume that the internal force in bar (3) is tension. From equilibrium, the force in bar (3) is
3
3
42 kN 42 kN (C)
F x F R
F R
The cross-sectional area of bar (3) is
( )
2 2 2 A 3 (^) = b 3 = 40 mm =1, 600 mm
The normal stress in bar (3) is
2 (^ )(^ ) 2 2 2
42 kN 1, 000 N/kN 26.250 MPa 1, 600
26.3 MPa (C) mm
F
A
σ
= = = − = Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
( )( )
2 2 2
2 2 (^2 ) 2
5 kN 1, 000 N/kN 736.364 mm 6.7901 N/mm
F
A
F
A
σ
σ
The width of bar (2) is therefore:
2 b 2 (^) = 736.364 mm = 27.136 mm = 27.1 mm Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
P1.6 Axial loads are applied with rigid bearing plates to the solid cylindrical rods shown in Figure
P1.6/7. One load of P = 1,500 lb is applied to the assembly at A , two loads of Q = 900 lb are applied
at B , and two loads of R = 1,300 lb are applied at C. The diameters of rods (1), (2), and (3) are d 1 =
0.625 in., d 2 = 0.500 in., and d 3 = 0.875 in. Determine the axial normal stress in each of the three
rods.
FIGURE P1.6/
Solution
Cut an FBD through rod (1). The FBD should include the free end of the assembly at A. We will
assume that the internal force in rod (1) is tension. From equilibrium, the force in rod (1) is
1
1
1,500 lb 1,500 lb (T)
F x P F
F P
Use the given diameter to calculate the cross-sectional area of rod (1):
( )
2 2 2 1 1 0.625 in.^ 0.3068 in. 4 4
A d
The normal stress in rod (1) is
1 (^1 ) 1
4,890 psi (T
1,500 lb 4,889.24 psi 0.3068 i
n.
F
A
σ = = = = Ans.
Cut an FBD through rod (2). The FBD should include the free end of the assembly at A. We will
assume that the internal force in rod (2) is tension. From equilibrium, the force in rod (2) is
( )
2
2
2 1,500 lb 2 900 lb 300 lb 300 lb (C)
F x P Q F
F P Q
Use the given diameter to calculate the cross-sectional area of rod (2):
( )
2 2 2 2 2 0.500 in.^ 0.1963 in. 4 4
A d
The normal stress in rod (2) is
2 (^2 ) 2
1,528 psi (
300 lb 1,527.89 psi C) 0.1963 in.
F
A
σ
= = = − = Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
Cut an FBD through rod (3). The FBD should include the free end of the assembly at A. We will
assume that the internal force in rod (3) is tension. From equilibrium, the force in rod (3) is
( ) ( )
3
3
2 2 1,500 lb 2 900 lb 2 1,300 lb 2,300 lb 2,300 lb (T)
F x P Q R F
F P Q R
Use the given diameter to calculate the cross-sectional area of rod (3):
( )
2 2 2 3 3 0.8750 in.^ 0.6013 in. 4 4
A d
The normal stress in rod (3) is
3 (^3 ) 3
3,820 psi (T
2,300 lb 3,824.92 psi 0.6013 i
n.
F
A
σ = = = = Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
P1.7 Axial loads are applied with rigid bearing plates to the solid cylindrical rods shown in Figure
P1.6/7. One load of P = 30 kips is applied to the assembly at A , two loads of Q = 25 kips are applied
at B , and two loads of R = 35 kips are applied at C. The normal stress magnitude in aluminum rod (1)
must be limited to 20 ksi. The normal stress magnitude in steel rod (2) must be limited to 35 ksi. The
normal stress magnitude in brass rod (3) must be limited to 25 ksi. Determine the minimum diameter
required for each of the three rods.
FIGURE P1.6/
Solution
Cut an FBD through aluminum rod (1). The FBD should include the free end of the assembly at A.
We will assume that the internal force in rod (1) is tension. From equilibrium, the force in rod (1) is
1
1
30 kips 30 kips (T)
F x P F
F P
The normal stress magnitude in aluminum rod (1) must be limited to 20 ksi. Therefore, the minimum
cross-sectional area of rod (1) must be
1 2 1 1
30 kips 1.500 in. 20 ksi
F
A
σ
The diameter must be
2 1 1
2 1
1.500 in. 1.382 in.
A d
d
∴ ≥ = Ans.
Cut an FBD through steel rod (2). The FBD should include the free end of the assembly at A. We
will assume that the internal force in rod (2) is tension. From equilibrium, the force in rod (2) is
( )
2
2
2 30 kips 2 25 kips 20 kips 20 kips (C)
F x P Q F
F P Q
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
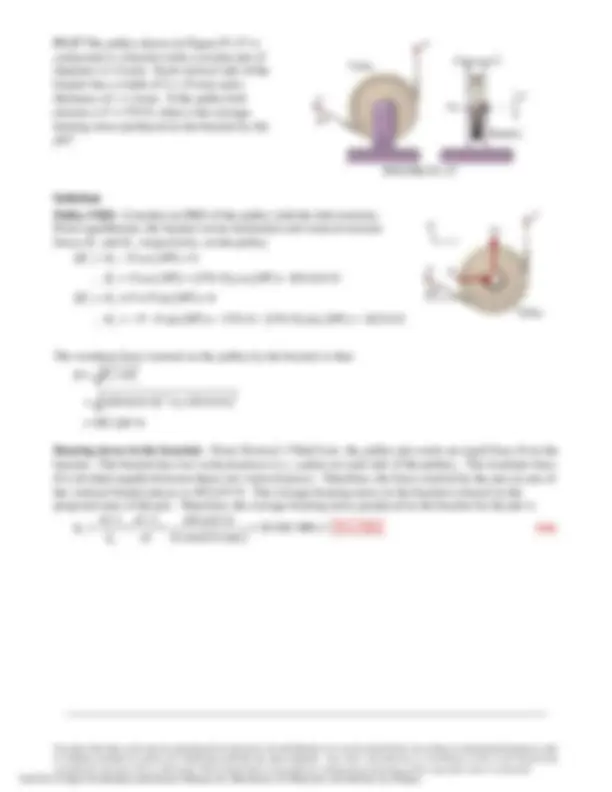
P1.8 Determine the normal stress in rod (1) for the
mechanism shown in Figure P1.8. The diameter of
rod (1) is 8 mm, and load P = 2,300 N. Use the
following dimensions: a = 120 mm, b = 200 mm, c =
170 mm, and d = 90 mm.
FIGURE P1.
Solution
First, consider an FBD of the pulley to determine the reaction forces exerted on the pulley by the
mechanism.
( )
( ) ( ) ( )
( )
( ) ( )
cos 60 0
2,300 N 2,300 N cos 60 3, 450.000 N
sin 60 0
2,300 N sin 60 1,991.858 N
x x
x
y y
y
F A P P
A
F A P
A
FBD of pulley FBD of mechanism
Next, consider an FBD of the mechanism to determine the force in rod (1). Rod (1) is oriented at an
angle of:
170 mm 90 mm tan 1. 200 mm
c d
b
b
b
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
Rod (1) is a two-force member, and its axial force can be calculated from:
( )( )
( )
( )( ) ( )( )
( ) ( )
1
1
cos 0
3, 450.000 N 170 mm 1,991.858 N 120 mm 5, 207.523 N cos 170 mm 90 mm cos 52.
C x y
x y
M A c A a F c d
A c A a F c d
b
b
The area of rod (1) is
( )
2 2 2 1 1 8 mm^ 50.265 mm 4 4
A d
The normal stress in the rod is thus
1 (^1 ) 1
5, 207.532 N
= 103.601 MPa
mm
3.6 MPa
F
A
σ = = = Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
P1.10 The rigid beam BC shown in Figure P1.10 is
supported by rods (1) and (2) that have diameters of
0.875 in. and 1.125 in., respectively. For a uniformly
distributed load of w = 4,200 lb/ft, determine the
normal stress in each rod. Assume L = 14 ft and a = 9
ft.
FIGURE P1.
Solution
Equilibrium: Calculate the internal forces in rods (1) and (2).
( ) ( )( )
( ) ( )( )
1
2
1
2
9 ft 14 ft 4, 200 lb/ft 9 ft 0 2
9 ft 14 ft 4, 200 lb/ft 9 ft 14 ft 0 2
12.150 kips
25.650 kips
C
B
F
M F
F
F
M
Areas:
( )
( )
(^2 ) 1
(^2 ) 2
0.875 in. 0.601 in. 4
1.125 in. 0.994 in. 4
A
A
Stresses:
1 (^1 ) 1
12.150 kips 20.206 ksi
20.2 ks i
i n.
F
A
σ = = = = Ans.
2 (^2 ) 2
25.650 kips 25.804 ksi
25.8 ks i
i n.
F
A
σ = = = = Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
P1.11 The rigid beam ABC shown in Figure P1.11 is
supported by a pin connection at C and by steel rod
(1), which has a diameter of 10 mm. If the normal
stress in rod (1) must not exceed 225 MPa, what is the
maximum uniformly distributed load w that may be
applied to beam ABC? Use dimensions of a = 340
mm, b = 760 mm, and c = 550 mm.
FIGURE P1.
Solution
The cross-sectional area of rod (1) is
(^2 ) 1 10 mm^ 78.540 mm 4
A
π = =
Since the normal stress in rod (1) must not exceed 225 MPa, the allowable force that can be applied to
rod (1) is:
2 2 F 1,allow (^) = σ 1 A 1 = 225 N/mm 78.540 mm =17, 671.459 N
Rod (1) is oriented at an angle of b with respect to the horizontal direction:
550 mm tan 0.7237 35. 760 mm
c
b
b= = = ∴ b= °
Consider an FBD of rigid beam ABC. From the moment
equilibrium equation about joint C , the relationship between
the force in rod (1) and the distributed load w is:
1
1 2
sin 0 2
2 sin
C
a b M w a b F b
b F w a b
b
b
Substitute the allowable force F 1,allow into this relationship to obtain the maximum distributed load that
may be applied to the structure:
1 2
2
2 sin
2 760 mm 17, 671.459 N sin 35.
340 mm 760 mm
13.0 14 N/mm 13.01 kN/m
b F w a b
b = + ° = +
= = Ans.
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
Joint A:
Begin the solution process by considering an FBD of joint A.
Consider only those forces acting directly on joint A. In this instance,
two axial members, AB and AC , are connected at joint A. Tension
forces will be assumed in each truss member.
Σ F x = FAB + FAC cos θ AC = 0 (a)
Σ F (^) y = FAC sin θ AC − P = 0 (b)
Solve Eq. (b) for FAC :
( )
200 kN
sin sin 53.
AC 250.0 kN AC
P
F
and then compute FAB using Eq. (a):
( ) ( )
cos
250.0 kN cos 53.13 0 150. 0 kN
F AB = − FAC θ AC
Joint D:
Next, consider an FBD of joint D. As before, tension forces will be
assumed in each truss member.
Σ F (^) x = Dx − FCD = 0 (c)
Σ F (^) y = Dy − FBD = 0 (d)
Solve Eq. (c) for FCD :
FCD = Dx = 400.0 kN
and solve Eq. (d) for FBD :
FBD = Dy = 200.0 kN
Joint C:
Next, consider an FBD of joint C. As before, tension forces will be
assumed in each truss member.
Σ F (^) x = FCD + FBC cos θ BC − FAC cos θ AC = 0 (e)
Σ F (^) y = − FBC sin θ BC − FAC sin θ AC = 0 (f)
Solve Eq. (e) for FBC :
( )
( )
( )
sin sin 53. 250 kN sin sin 38.
BC AC AC 320.1562 kN BC
F F
θ
θ
Eq. (f) can be used as a check on our calculations:
( ) ( ) ( ) ( )
sin sin
320.1562 kN sin 38.660 250.0 kN sin 53.130 0
Σ F y = − FBC θ BC − FAC θ AC
= − − ° − ° = Checks!
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis for testing or instructional purposes only to students enrolled in courses for which the textbook has been adopted. Any other reproduction or translation of this work beyond that
permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful.
Section properties:
For each of the five truss members:
( ) ( ) ( )
(^2 2 ) 115 mm 2 6 mm 103 mm 115 mm 103 mm 2, 054.602 mm 4
d A
= − = = ^ − =
Normal stress in each truss member:
( )( ) 2
150 kN 1,000 N/kN 73.007 MPa 2, 054.
73.0 MPa 602 m
(C)
m
AB AB AB
F
A
σ
= = = − = Ans.
( )( ) 2
250.0 kN 1,000 N/kN 121.678 MPa 2, 054.
121.7 MP
a ( 0 m
T)
2 m
AC AC AC
F
A
σ = = = = Ans.
( )( ) 2
320.156 kN 1,000 N/kN 155.824 MPa 2, 054
155.8 MP
m
a C m
BC BC BC
F
A
σ
= = = − = Ans.
( )( ) 2
200.0 kN 1,000 N/kN 97.342 MPa 2, 054
97.3 MPa (T) .602 mm
BD BD BD
F
A
σ = = = = Ans.
( )( ) 2
400.0 kN 1,000 N/kN 194.685 MPa 2, 054.
194.7 MP
a ( 0 m
T)
2 m
CD CD CD
F
A
σ = = = = Ans.
