








Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity

Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium


Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Prepara tus exámenes con los documentos que comparten otros estudiantes como tú en Docsity
Los mejores documentos en venta realizados por estudiantes que han terminado sus estudios
Estudia con lecciones y exámenes resueltos basados en los programas académicos de las mejores universidades
Responde a preguntas de exámenes reales y pon a prueba tu preparación

Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Comunidad
Pide ayuda a la comunidad y resuelve tus dudas de estudio
Descubre las mejores universidades de tu país según los usuarios de Docsity
Ebooks gratuitos
Descarga nuestras guías gratuitas sobre técnicas de estudio, métodos para controlar la ansiedad y consejos para la tesis preparadas por los tutores de Docsity
El resultado de la práctica realizada en la materia de Estadística Administrativa 1, en la que se determina el número de primos por cada alumno del grupo 2A, mediante la distribución de frecuencias. Se calculan y presentan las medidas de tendencia central y dispersion, como media, mediana, moda, rango y varianza. Además, se presentan diferentes tipos de graficas para interpretar los resultados.
Qué aprenderás
Tipo: Guías, Proyectos, Investigaciones
1 / 14

Esta página no es visible en la vista previa
¡No te pierdas las partes importantes!









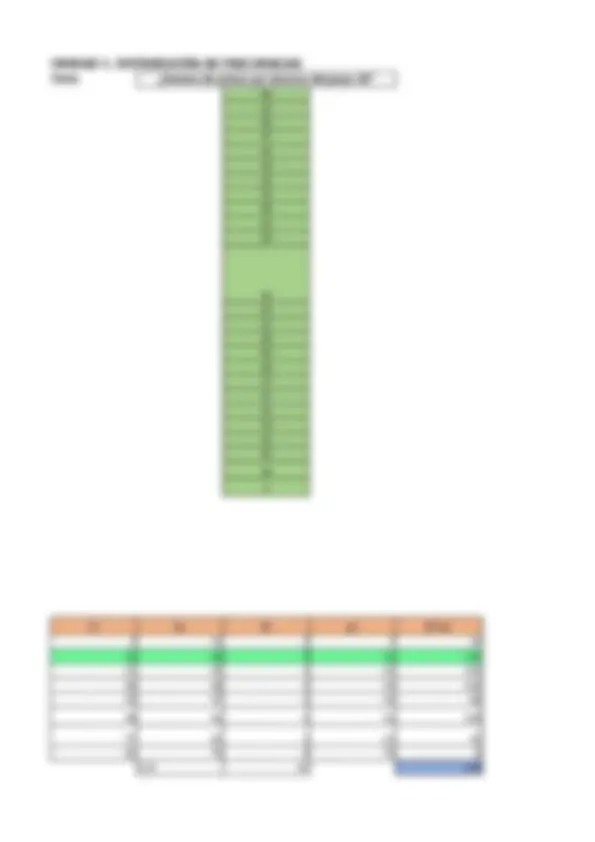
PRÁCTICA: DISTRIBUCIÓN DE FRECUENCIAS
26.8 (^) MEDIA 7 17 27 37 47 57 67 0 1 2 3 4 5 6 7 8 9 10
ENCONTRAR EL VALOR MAXIMO ENCONTRAR EL VALOR MINIMO TABLA DE DATOS n 25 Numero total de observaciones V.MAX 60 valor maximo V.MIN 3 valor minimo r 57 rango denominador r/1+3.332*LOG(n) I.C. AMPLITUD RANGO/K redondeo LIMITE INF. LIMITE SUP. MARCA CLASE 1 3 11 2 0 2 2 12 20 9 7 11 3 21 29 5 16 16 4 30 38 4 25 20 5 39 47 2 34 22 6 48 56 2 43 24 7 57 65 1 52 25 8 66 74 0 61 25 TOTALES 25 70 DATOS DATOS Li 16 Li 3 faa 2 ∆1 7 fm 9 ∆2 4 ic 8 ic 8 N 25
25.3333333333333 8. Multimodales 22 20 NUMERO DE CLASES FRECUENCIA ABSOLUTA FRECUENCIA ABSOLUTA ACUMULADA INTERPRETACIÓN:
60 3 r maximo r minimo rango
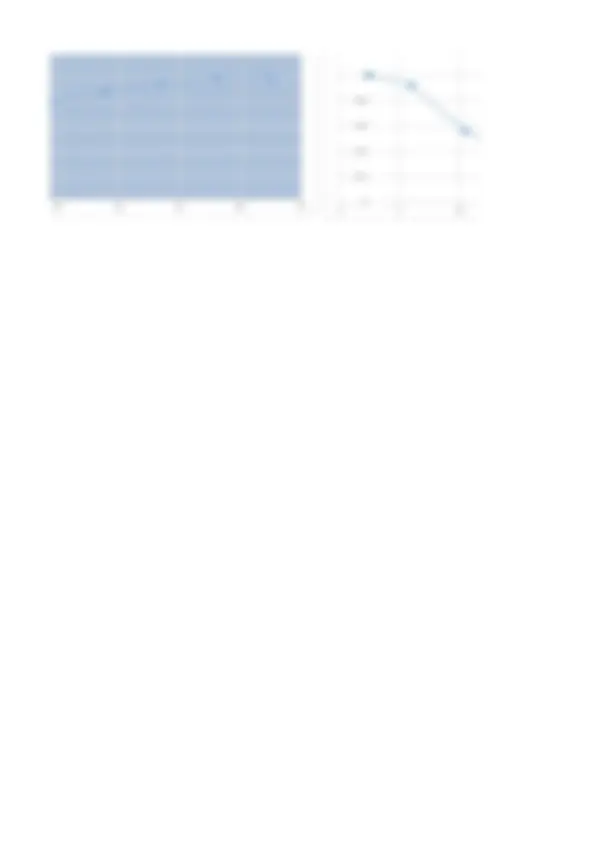
8 0.08 0 1 0.36 0.08 0. 0.2 0.44 0. 0.16 0.64 0. 0.08 0.8 0. 0.08 0.88 0. 0.04 0.96 0. 0 1 0 1 1 0 FRECUENCIA RELATIVA FRECUENCIA RELATIVA ACUMULADA FRECUENCIA RELATIVA ACUMULADA INVERSA 11 20 29 38 47 0 1 2 3 4 5 6 7 8 9 10 GRÁFICA DE BARR NUMERO DE PRIMOS POR ALUMN GRAFICA DE BARRAS 7 1 7 2 7 3 7 4 0 1 2 3 4 5 6 7 8 9 10 POLIGONO DE FRECUEN NUMERO DE PRIMOS POR ALUMNO
1
OJIVA MENOR QU NUMERO DE PRIMOS POR ALUMN
OJIVA MENOR QU
- 392.04 784. - 116.64 1049. - 3.24 16. - 51.84 207. - 262.44 524. - 635.04 1270. - 1169.64 1169. - 1866.24 5 35 45 55 65 75 IVA MENOR QUE OS POR ALUMNO DEL GRUPO 2A -5 5 15 25 35
OJIVA MAYO NUMERO DE PRIMOS POR A
16 25 34 43 52 61 70 HI STOGRA MA ERO DE PRI MOS POR ALUMNO DEL GRUPO 2 A Column I 8.00% 36.00% 20.00% 16.00% 8.00% 8.00%4.00%
1 2 3 4 5 6 7 8 OJIVA MAYOR QUE UMERO DE PRIMOS POR ALUMNO DEL GRUPO 2A
CONCLU En el ejercicio hizimos la pregunta sobre cuantos primos a distribución de frecuencias, el cual nos dio 8 numero hacer una comparación adecuada, realizamos sus r importante, ya que sin las interpretaciones no sirven calculamos su media, mediana, moda, rango y varianza poligono de fre La distribución de frecuencia nos facilita la obtencion diferentes tipos de frecuencias; por ejemplo, frecuenc acumulada y relativa acumulada inversa., en e Las medidas de tendencia central consiste en la m La medidas de dispersion consis CONCLU En el ejercicio hizimos la pregunta sobre cuantos primos a distribución de frecuencias, el cual nos dio 8 numero hacer una comparación adecuada, realizamos sus r importante, ya que sin las interpretaciones no sirven calculamos su media, mediana, moda, rango y varianza poligono de fre La distribución de frecuencia nos facilita la obtencion diferentes tipos de frecuencias; por ejemplo, frecuenc acumulada y relativa acumulada inversa., en e Las medidas de tendencia central consiste en la m La medidas de dispersion consis
ONCLUSIÓN bre cuantos primos tiene cada alumno del grupo 2A para poder hacer un al nos dio 8 numeros de clases, las mismas que nos sirvio para poder a, realizamos sus respectivas graficas y las interpretamos, esto es taciones no sirven de alguna manera efectiva las graficas, posterior a, rango y varianza, al final señalamos la media, mediana y moda en el poligono de frecuencias. acilita la obtencion de la informacion que contiene los datos, existen r ejemplo, frecuencia absoluta, absoluta acumulada, relativa, relativa ulada inversa., en este caso se realizo con datos agrupados. ral consiste en la media aritmetica, ponderada, mediana y moda. e dispersion consiste en el rango y la varianza. ONCLUSIÓN bre cuantos primos tiene cada alumno del grupo 2A para poder hacer un al nos dio 8 numeros de clases, las mismas que nos sirvio para poder a, realizamos sus respectivas graficas y las interpretamos, esto es taciones no sirven de alguna manera efectiva las graficas, posterior a, rango y varianza, al final señalamos la media, mediana y moda en el poligono de frecuencias. acilita la obtencion de la informacion que contiene los datos, existen r ejemplo, frecuencia absoluta, absoluta acumulada, relativa, relativa ulada inversa., en este caso se realizo con datos agrupados. ral consiste en la media aritmetica, ponderada, mediana y moda. e dispersion consiste en el rango y la varianza.