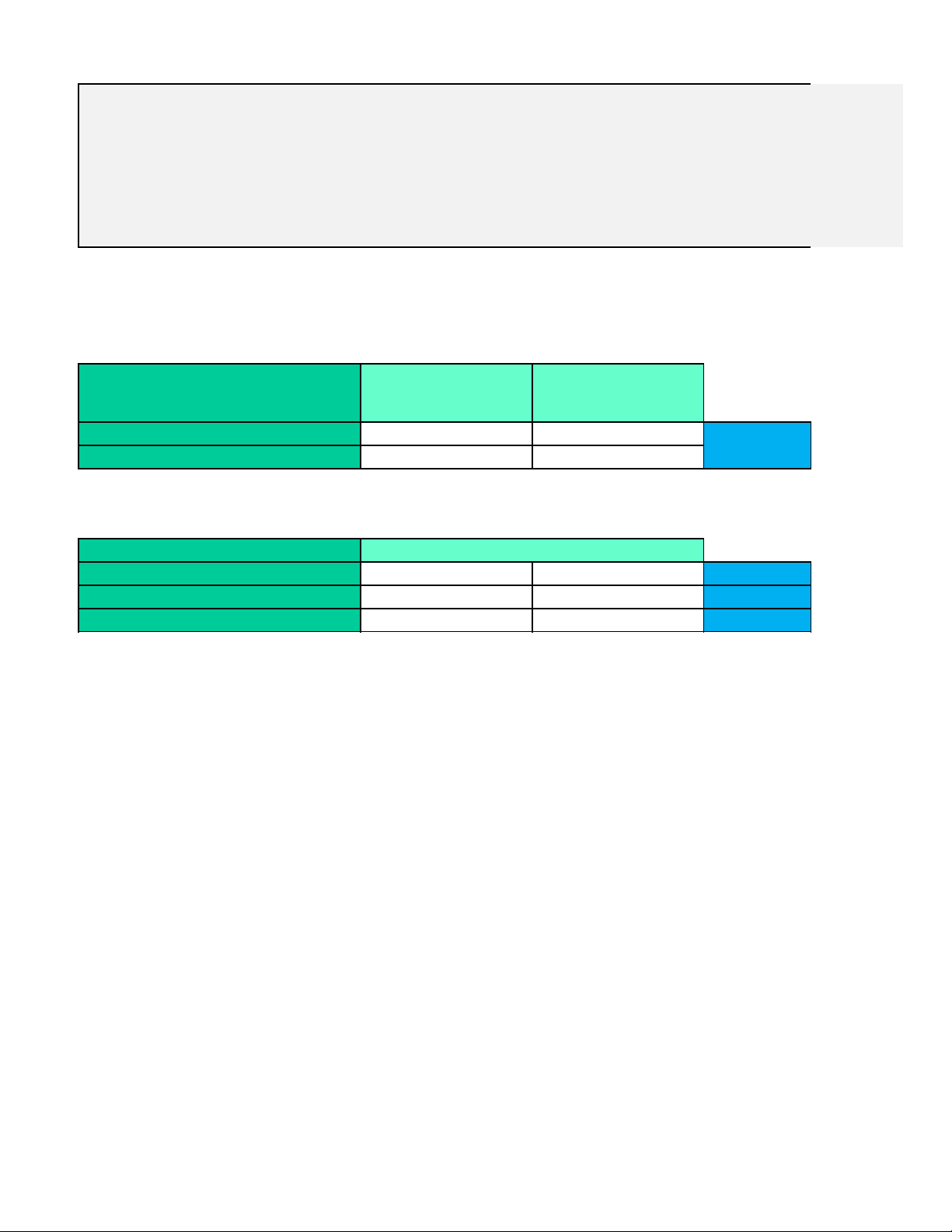
F. O / Variable decisión
Solucion optima 6 3
45Máx. Utilidades $ 5 $ 5
Recursos / Variables Actividades
Unidad de material 12 8 96
Horas de mano de obra 6 12 72
Mesas prometidas por el fabricante 1 0 6
4. Un fabricante está tratando de decidir sobre las cantidades de producción para dos artículos: mesas y sillas. Se cuenta con 96 unidades de material y con 72 horas de mano de
obra. Cada mesa requiere 12 unidades de material y 6 horas de mano de obra. Por otra parte, las sillas usan 8 unidades de material cada una y requieren 12 horas de mano de
obra por silla. El margen de contribución es el mismo para las mesas que para las sillas: $5.00 por unidad. El fabricante prometió construir por lo menos dos mesas y su objetivo
es maximizar la contribución a la ganancia.
Cantidad de mesas a
producir
Cantidad de sillas a
producir
