material didactico ,,,,,,,, Apuntes de Matemática Financiera

¡Descarga material didactico ,,,,,,, y más Apuntes en PDF de Matemática Financiera solo en Docsity!

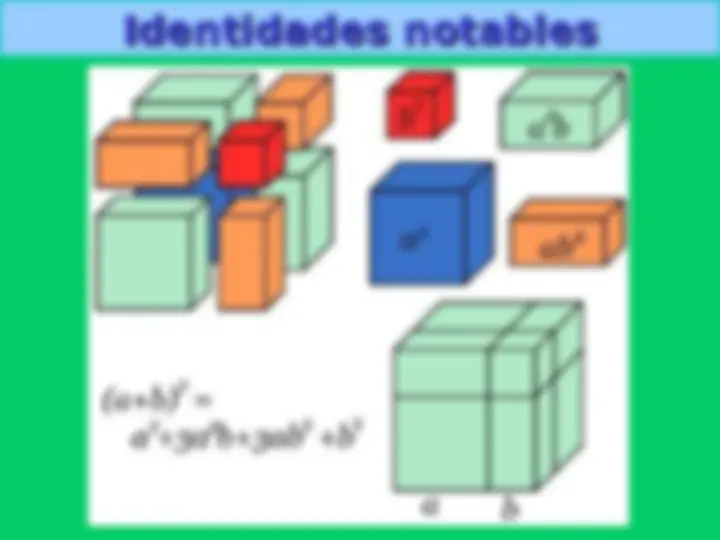
Los polinomios son una parte importante del Álgebra. Están presentes en todos los contextos científicos y tecnológicos: desde los ordenadores y la informática hasta la carrera espacial. La fórmula que expresa el movimiento de un cuerpo en caída libre viene dada por el siguiente polinomio: 2 2 1 P ( t ) gt t: tiempo g: gravedad La fórmula para calcular el volumen de un cubo en función de la longitud ( l ) de su lado viene dada por: 3 V ( l )  l

Partes de un monomioPartes de un monomio Los coeficientes son los números que aparecen multiplicando. La parte literal la forman las letras y sus exponentes. El grado del monomio es la suma de los exponentes de las letras. Gr.  2 Gr.  3  1  2  6 Gr.  1  1  15  17 (^1 1 )

Tipos de monomiosTipos de monomios Monomios semejantessemejantes: tienen la misma parte literal. Monomios opuestosopuestos: son semejantes y sus coeficientes son números opuestos. NO semejantes NO opuestos 3 2  25 a b 2 3 a b c 25 a b 2 3 3 2 3 a b 2 3  25 a b 2 3 a b 5 xy xy 7 1  2 3  25 a b 2 3 25 a b 3 2 7 1  x y 3 2 7 1 x y 2 3 a b 2 3 a b xy (^) xy  

Operaciones con monomiosOperaciones con monomios Para multiplicarmultiplicar por un lado, multiplicamos sus coeficientes y, por otro, sus partes literales. 4 2  15 x y Ejemplo 3:  3 y  7 y  2 Ejemplo 4:  3  7 2 y y 3 ( )  21 y   2 3 55 xy  33 x (^ ) 2 xy 3 x

Operaciones con monomiosOperaciones con monomios Para dividirdividir por un lado, dividimos sus coeficientes y, por otro, sus partes literales (si se puede). Ejemplo 5: Ejemplo 6:   7 2 21 y : 7 y 25 a b : 4 b  3 2  21 : 7 (^ )^ (^ ) 7 y 2 y : 5  3 y 25 a b 4 3 b 3 4 25  a

PolinomiosPolinomios El valor numéricovalor numérico de un polinomio P(x), para un valor x=a, lo expresamos como P(a) y se obtiene sustituyendo la variable x por el valor a en el polinomio y operando. ( ) 7 3 4 10 4 3 P x  x  x  x  ( 2 )  7  2  3  2  4  2  10  4 3 P (  1 )  7 ^ ^1 ^  3 ^1 ^  4 ^1 ^  10  4 3 P Ejemplo :  7  16  3  8  8  10  112  24  8  10  86  7  1  3   1   4  10  7  3  4  10  4

PolinomiosPolinomios El polinomio opuestopolinomio opuesto de un polinomio P(x), que designamos como -P(x), se obtiene cambiando el signo de todos los términos de P(x). ( ) 7 3 4 10 4 3 P x  x  x  x  ( ) 7 3 4 10 4 3  P x  x  x  x  Ejemplo : Polinomio opuesto:

Operaciones con polinomiosOperaciones con polinomios Para restarrestar polinomios sumamos al primero el opuesto del segundo. Ejemplo: (^) ( ) 2 7 1 5 4 2 P x  x  x  x  ( ) 3 2 2 7 8 4 3 2 Q x  x  x  x  x  P ( x )  Q ( x ) 5 2 x 4  x 2  7 x  1 4  3 x 3  2 x 2  2 x  7 x  8 2 4 2 9 7 9 5 4 3 2 x  x  x  x  x 

Operaciones con polinomiosOperaciones con polinomios Para multiplicar un monomio por un polinomiomultiplicar un monomio por un polinomio multiplicamos el monomio por cada uno de los términos del polinomio. Ejemplo: 5 4 2 3 P ( x )  2 x  x  7 x  1 por 2 x 2 ( ) 3 x  P x 3 2 x 8 7 5 3 4 x  2 x  14 x  2 x

5 4 2 x  x  x 

Operaciones con polinomiosOperaciones con polinomios Para dividir un polinomio entre un monomiodividir un polinomio entre un monomio , dividimos cada término del polinomio entre el monomio. (^) Ejemplos: 5 4 2 P ( x )  6 x  9 x  27 x

2 3 9 ( ) : 3 6 : 3 9 : 3 27 : 3 3 2 2 5 2 4 2 2 2        x x P x x x x x x x x Q ( x ) 7 x y 5 xy 3  

3 2 7 5 7 5 ( ) : 2 2 2 2 2 x y xy Q x x x y y x x       

Operaciones con polinomiosOperaciones con polinomios Para dividir un polinomio entre un polinomiodividir un polinomio entre un polinomio , seguiremos los siguientes pasos: 1º) Ordenamos los términos del dividendo y del divisor y los dispondremos como una división normal. P ( x ) 2 x x 20 11 x 30 x 3 4 2      ( ) 3 2 2 Q x  x  x  3  2 x 4 x 2  11 x  30 x  20 2 x  3 x  2

Operaciones con polinomiosOperaciones con polinomios 3  2 x 4 x 2  11 x ^30 x ^20 2 x ^3 x  2 4º) Se suman algebraicamente. 5º) Se divide el primer término del nuevo residuo, entre el primer término del divisor, así obtenemos el segundo término del divisor. Este segundo término se multiplica por el divisor y se pasa 2 x 4 3 2  x  3 x  2 x 5 9 30 20 3 2  x  x  x   5 x x x x x x x 5 15 10 5 3 2 3 2 2        5 x 15 x 10 x 3 2  

Operaciones con polinomiosOperaciones con polinomios 6º) Se repite el procedimiento hasta que el grado del polinomio resto sea menor que el grado del polinomio divisor. 3  2 x 4 x 2  11 x  30 x  20 2 x  3 x  2 2 x 4 3 2  x  3 x  2 x 5 9 30 20 3 2  x  x  x   5 x 5 x 15 x 10 x 3 2   6 20 20 2 x  x 

6 18 12 2  x  x  2 x  8