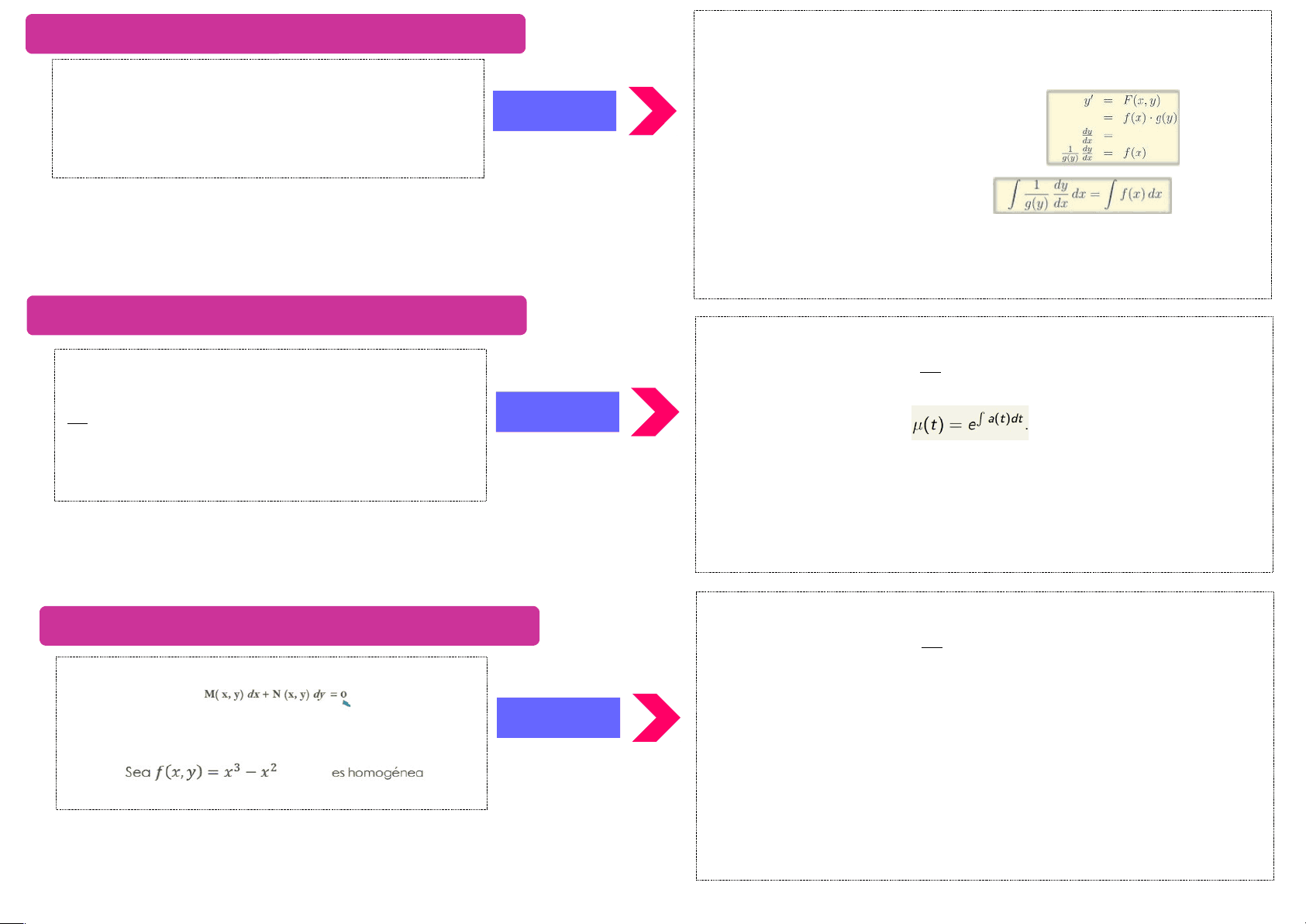
Paso 1: Factorizar el segundo miembro
Factorizar
F
(
x , y
)
=f
(
x
)
. g(y)
, si tal factorizacion no es posible se concluye
que la ED no es de variables separables y el procedimiento no continua.
Paso 2: separar las variables
Hacer algebra para poner variables diferentes en lados diferentes
Paso 3: integrar
Integrando la opcion interior con respecto a x obtenemos
Paso 4: despejar y opcional
Debido a que Y representa la funcion incognita a determinar lo ideal
es determinarla por completo, en su expresion:
y
´
=expresionen x
procedimient
o
Una ecuacion diferencial de primer orden de la forma:
y
´
=F(x , y )
Se dice de variables separables si es posible factorizar
F(x, y)
en la forma:
Ecuaciones diferenciales de variables separables
y
´
=F(x , y )
Para calcular la soluci´on expl´ıcita de una ecuaci´on lineal del tipo:
dy
dt =g
(
t
)
. y+r(t)
Paso 1: calcular el factor de integracion
Paso 2: multiplicacion de miembros
Multiplicamos ambos miembros de la ecuaci´on diferencial lineal por dicho
factor de integraci´on
Paso 3: integrar
Para calcular la soluci´on expl´ıcita de una ecuaci´on lineal del tipo:
dy
dt =g
(
t
)
. y+r(t)
Paso 1: calcular el factor de integracion
Paso 2: multiplicacion de miembros
Multiplicamos ambos miembros de la ecuaci´on diferencial lineal por dicho
factor de integraci´on
Paso 3: integrar
Integrando la ecuacion.
procedimient
o
A partir de una ecuacion diferencial
Se dice que son homogeneas si M y N son funcionales
homogeneas del mismo grado
Ecuaciones homogéneas
procedimient
o
Ecuaciones lineales
Una ecuaci´on diferencial de primer orden es lineal si
puede escribirse en la forma:
dy
dt =g
(
t
)
. y+r(t)
La palabra lineal en el nombre de la ecuaci´on se refiere
al hecho de que la variable dependiente y aparece en la
ecuaci´on elevada solo a la primera potencia. La ecuaci
