Función Lineal
Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Orientación Universidad
Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Busca documentos
Prepara tus exámenes con los documentos que comparten otros estudiantes como tú en Docsity
Busca documentos en el Store
Los mejores documentos en venta realizados por estudiantes que han terminado sus estudios
Video Cursos
Estudia con lecciones y exámenes resueltos basados en los programas académicos de las mejores universidades
Quiz
Responde a preguntas de exámenes reales y pon a prueba tu preparación
Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Comunidad
Pregúntale a la comunidad
Pide ayuda a la comunidad y resuelve tus dudas de estudio
Ranking de las universidades
Descubre las mejores universidades de tu país según los usuarios de Docsity
Ebooks gratuitos
¡Nuestros e-books salva-estudiantes!
Descarga nuestras guías gratuitas sobre técnicas de estudio, métodos para controlar la ansiedad y consejos para la tesis preparadas por los tutores de Docsity
Funciones lineales y afines - Prof. Morillo, Esquemas y mapas conceptuales de Teoría combinatoria
Este documento proporciona una introducción a las funciones lineales y afines, incluyendo sus características, gráficas y ejemplos. Cubre diferentes tipos de funciones lineales, como las de dominio acotado y las de dominio partido. Además, presenta ejercicios para determinar los parámetros de funciones lineales y afines a partir de información dada. Útil para estudiantes que buscan comprender los conceptos básicos de las funciones lineales y afines, así como para aquellos que necesitan practicar la resolución de problemas relacionados con este tema. Puede ser utilizado como material de estudio, resumen o ejercicios en cursos de matemáticas a nivel universitario o de bachillerato.
Tipo: Esquemas y mapas conceptuales
2022/2023
1 / 17
Esta página no es visible en la vista previa
¡No te pierdas las partes importantes!
Documentos relacionados
Vista previa parcial del texto
¡Descarga Funciones lineales y afines - Prof. Morillo y más Esquemas y mapas conceptuales en PDF de Teoría combinatoria solo en Docsity!
Función Lineal
Función Lineal
La función lineal es del tipo: y = mx.
Su gráfica es una línea recta que pasa por el origen de coordenadas
Función Lineal-Afin
Ejemplos:
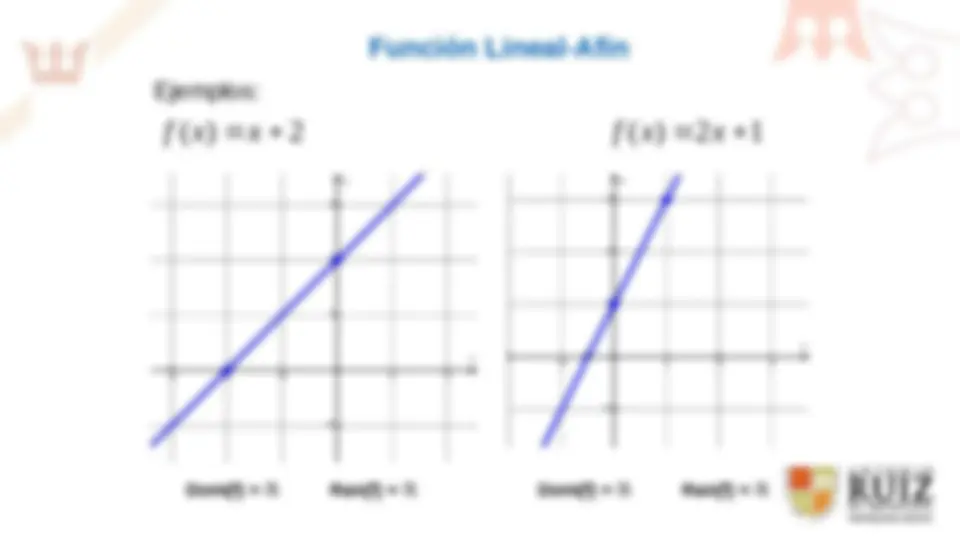
f ( x ) x 2 x y x y x y f ( x ) 2 x 1 x y x y x y
Dom(f) = ℝ Ran(f) = ℝ Dom(f) = ℝ Ran(f) = ℝ
Función lineal con dominio acotado
Es una función lineal cuyo dominio se encuentra
restringido a través de una desigualdad.
Ejemplos:
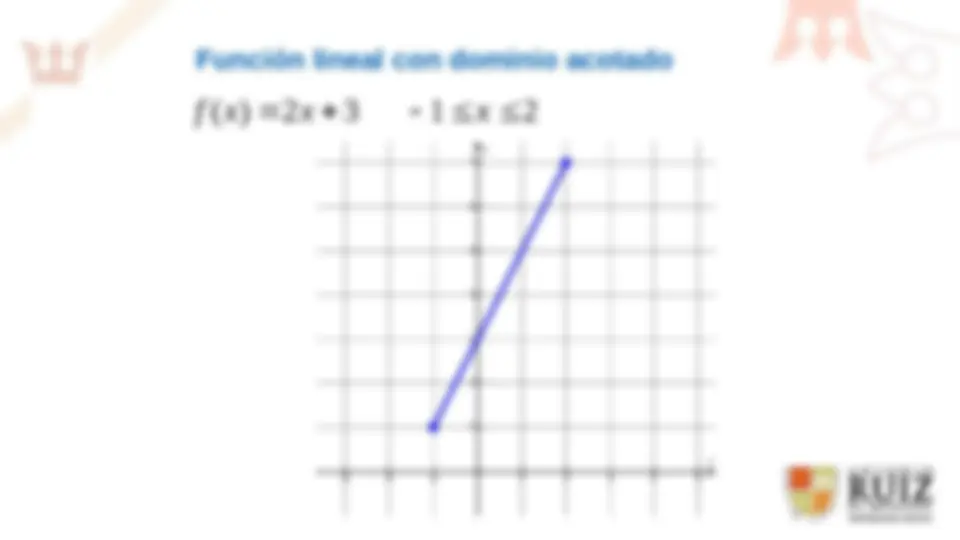
f ( x ) 2 x 3 ; 1 x 2
2 1 g ( x ) x x
1 ^0 ; 4 2 1 g ( x ) x x x y x y x y
Función lineal con dominio acotado
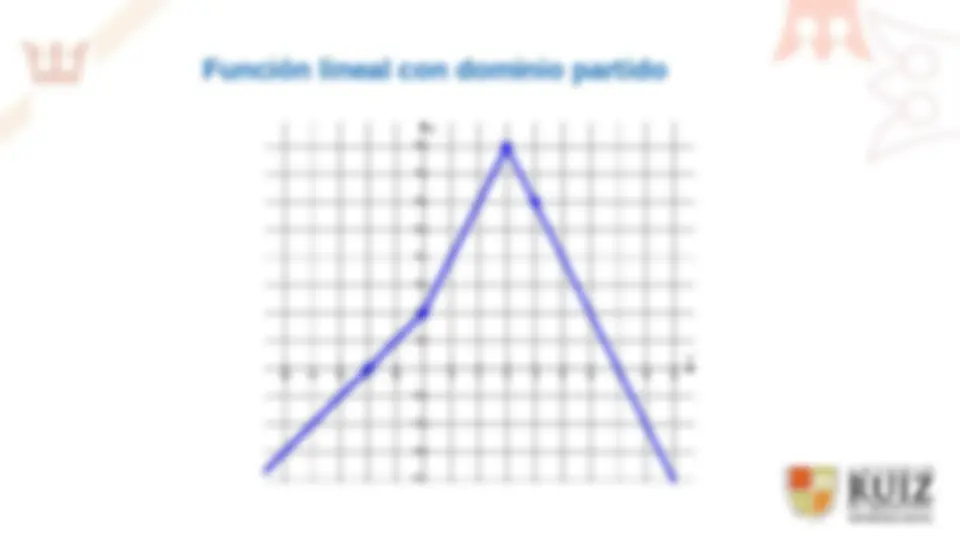
Función lineal con dominio partido
x y x y x y x y x y x y x y x y x y
Función lineal con dominio partido
Grafique la siguiente función e indique su rango:
x x
x
x x
f x
Función lineal
con dominio partido
1
De la función f(x) definida por:
se sabe que: f(-5) = 2; f(1) = 6 y que la gráfica de f(x) intersecta
al eje X en el punto de abscisa 6.
a) Determine las constantes k, m y b.
b) Grafique la función f. Geogebra
8 2 1 2 10 1 ( ) mx b x mx b x k x f x Rpta. a) k=2, m=2 y b=
Función lineal con dominio partido
2
La función f definida por:
cumple que a la imagen 2 le corresponden pre imágenes -1 y 1.
a) Determine los valores de a y b.
b) Trace la gráfica de f. Geogebra
Función lineal con dominio partido
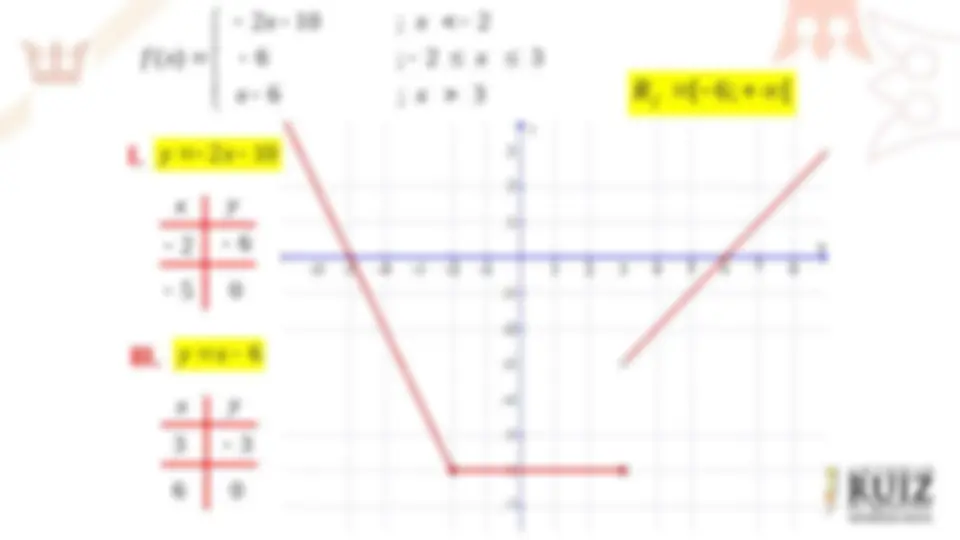
3 x b x ax x f x 2 ; 0 4 ; 3 0 ( )