


Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity

Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium


Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Prepara tus exámenes con los documentos que comparten otros estudiantes como tú en Docsity
Los mejores documentos en venta realizados por estudiantes que han terminado sus estudios
Estudia con lecciones y exámenes resueltos basados en los programas académicos de las mejores universidades
Responde a preguntas de exámenes reales y pon a prueba tu preparación

Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Comunidad
Pide ayuda a la comunidad y resuelve tus dudas de estudio
Descubre las mejores universidades de tu país según los usuarios de Docsity
Ebooks gratuitos
Descarga nuestras guías gratuitas sobre técnicas de estudio, métodos para controlar la ansiedad y consejos para la tesis preparadas por los tutores de Docsity
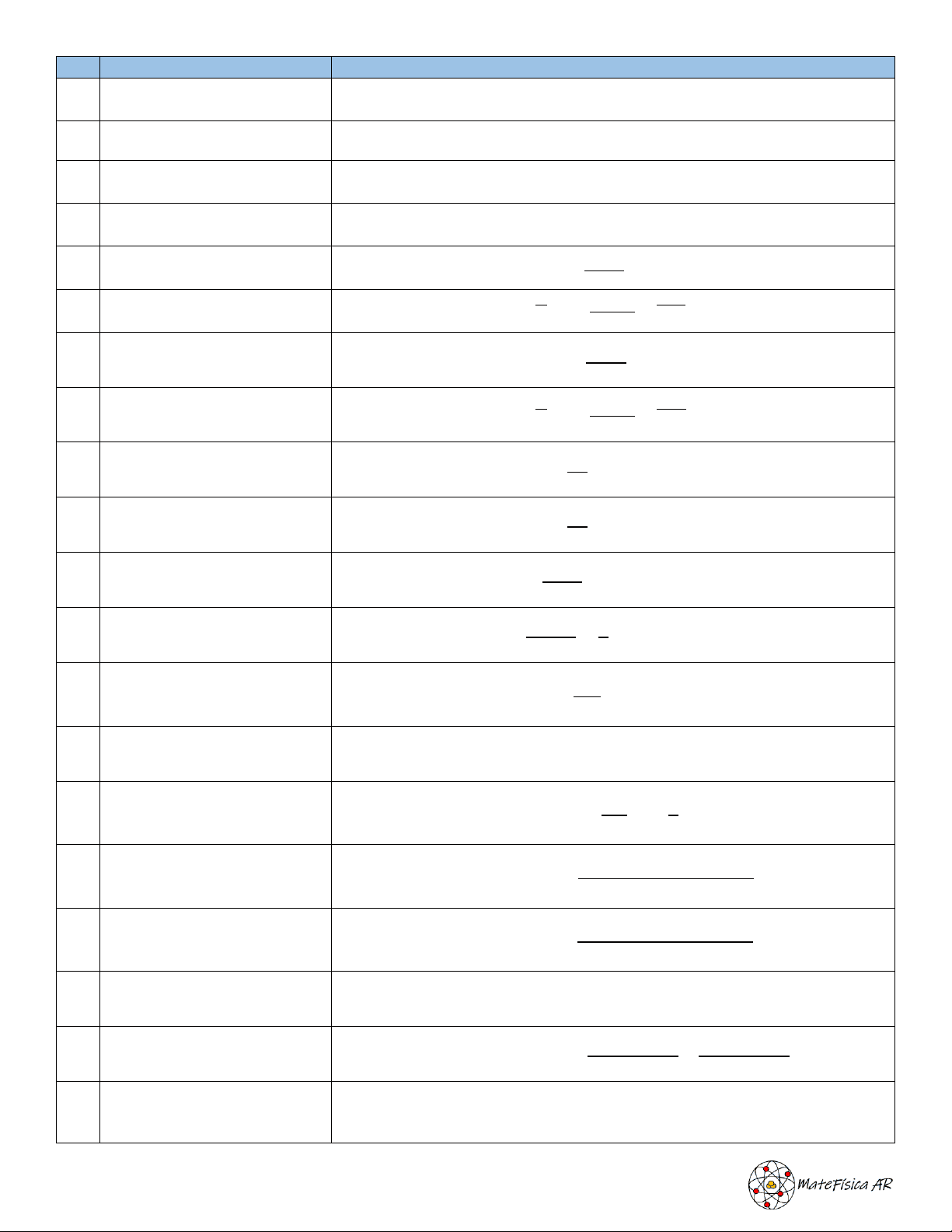
Fórmulas de las integrales para el desarrollo de ejercicios.
Tipo: Apuntes
1 / 3

Esta página no es visible en la vista previa
¡No te pierdas las partes importantes!


No. Nombre Formula
Integral del diferencial de una
variable
2 Integral de una constante ∫ 𝑘 𝑑𝑥 = 𝑘𝑥 + 𝐶
Integral de varios términos de
una función
Integral de una variable por
una constante
Integral de una variable con
un exponente entero
𝑛
𝑛+ 1
Integral de una variable con
exponente fraccionario
𝑚
𝑛 𝑑𝑥 =
𝑚+𝑛
𝑛
Integral de una nueva variable
con un exponente
𝑛
𝑛+ 1
Integral de una nueva variable
con exponente fraccionario
𝑚
𝑛
𝑑𝑥 =
𝑚+𝑛
𝑛
Integral de logaritmo natural
de una variable
= ln
Integral de logaritmo natural
de una nueva variable
= ln|𝑢| + 𝐶
Integral típica en fracciones
parciales
= ln
Integral de típica en fracciones
parciales II
ln|𝑎𝑥 ± 𝑘| + 𝐶
Integral de un exponencial
siendo a un entero diferente
de 1 y una función u
𝑢
𝑢
ln 𝑎
Integral de un exponencial con
el numero e y una función u
𝑢
𝑢
Integral por partes de un
exponencial con k como
constante
𝑎𝑥
𝑎𝑥
Integral por partes de un
exponencial por el seno
siendo a y b constantes
𝑎𝑥
𝑎𝑥
2
2
Integral por partes de un
exponencial por el coseno
siendo a y b constantes
𝑎𝑥
𝑎𝑥
2
2
18 Integral del logaritmo natural ∫ ln 𝑥 𝑑𝑥 = 𝑥 ∙ 𝑙𝑛
Integral del seno por el coseno
de una variable
cos(𝑎 − 𝑏) 𝑥
cos(𝑎 + 𝑏) 𝑥
Integral del seno de una
función
∫ 𝑠𝑒𝑛 𝑢 𝑑𝑢 = − cos 𝑢 + 𝐶
Integral del coseno de una
función
∫ cos 𝑢 𝑑𝑢 = 𝑠𝑒𝑛 𝑢 + 𝐶
Integral de la tangente de una
función
∫ tan 𝑢 𝑑𝑢 = ln | sec 𝑢| + 𝐶
Integral de la cotangente de
una función
∫ cot 𝑢 𝑑𝑢 = ln
Integral de la secante de una
función
∫ sec 𝑢 𝑑𝑢 = ln | sec 𝑢 + tan 𝑢| + 𝐶
Integral de la cosecante de
una función
∫ csc 𝑢 𝑑𝑢 = ln | csc 𝑢 − cot 𝑢| + 𝐶
Integral del seno al cuadrado
de una función
2
Integral del coseno al
cuadrado de una función
2
Integral de la tangente al
cuadrado de una función
2
𝑢 𝑑𝑢 = tan 𝑢 − 𝑢 + 𝐶
Integral de la cotangente al
cuadrado de una función
∫ cot
2
𝑢 𝑑𝑢 = − cot 𝑢 − 𝑢 + 𝐶
Integral de la secante al
cuadrado de una función
∫ sec
2
𝑢 𝑑𝑢 = tan 𝑢 + 𝐶
Integral de la cosecante al
cuadrado de una función
∫ csc
2
𝑢 𝑑𝑢 = − cot 𝑢 + 𝐶
Integral de la secante por
tangente de una función
∫ sec 𝑢 ∙ tan 𝑢 𝑑𝑢 = sec 𝑢 + 𝐶
Integral de la cosecante por
cotangente de una función
∫ csc 𝑢 ∙ cot 𝑢 𝑑𝑢 = −csc 𝑢 + 𝐶
Integral del seno hiperbólico
de una función
∫ 𝑠𝑒𝑛ℎ 𝑢 𝑑𝑢 = cosh 𝑢 + 𝐶
Integral del coseno hiperbólico
de una función
∫ cosh 𝑢 𝑑𝑢 = 𝑠𝑒𝑛ℎ 𝑢 + 𝐶
Integral de la tangente
hiperbólica de una función
∫ tanh 𝑢 𝑑𝑢 = ln | cosh 𝑢| + 𝐶
Integral de la cotangente
hiperbólica de una función
∫ coth 𝑢 𝑑𝑢 = ln|𝑠𝑒𝑛ℎ 𝑢| + 𝐶
Integral de la secante
hiperbólica de una función
∫ sech 𝑢 𝑑𝑢 = 𝑠𝑒𝑛
− 1
(tanh 𝑢) + 𝐶
Integral de la cosecante
hiperbólica de una función
∫ csch 𝑢 𝑑𝑢 = ln | tanh