¡Descarga Física I: Sistemas de Unidades, Vectores y Operaciones Vectoriales - Prof. Peña y más Apuntes en PDF de Física solo en Docsity!
Agosto 2023
Unidad 1. Física, mediciones y vectores
Física I
- Sistemas de unidades y estándares
- Fundamentos de la física: su naturaleza y cómo resolver problemas
- Homogeneidad dimensional y conversión de unidades
- Vectores y suma de vectores (representación gráfica, concepto de magnitud y de dirección)
- Incertidumbre y cifras significativas
- Suma analítica de vectores 6.1. Método del triángulo 6.2. Método de las componentes
- Producto vectorial
- Producto entre vectores
- Producto escalar
1. Fundamentos de la física: su naturaleza y cómo
resolver problemas
La física es una ciencia experimental ; en su ejercicio se observan los fenómenos naturales para intentar encontrar los patrones y principios que los describen. Tales patrones se denominan teorías físicas o, si están muy bien establecidos y se usan ampliamente, leyes o principios físicos. Cuidado con el significado de la palabra “teoría” en física. La palabra teoría no implica que se trate de una divagación o de un concepto no comprobado. Mas bien, una teoría es una explicación de fenómenos naturales basada en observaciones y en los principios fundamentales aceptados. Las leyes fundamentales de la física que se usan para elaborar teorías se expresan en el lenguaje de las matemáticas , la herramienta que proporciona un puente entre la teoría y el experimento
¿Cómo resolver problemas en física?
4 IDENTIFICAR los conceptos pertinentes: Primero, decida qué ideas de la física son relevantes para el problema. Aunque este paso no implica hacer cálculos, a veces es la parte más difícil. Nunca lo omita; si desde el principio se elige el enfoque equivocado, el problema se dificultará innecesariamente, e incluso podría llevar a una respuesta errónea. A estas alturas también se debe identificar la incógnita del problema; es decir, la cantidad cuyo valor se desea encontrar. En ocasiones, la meta será hallar una expresión matemática para la incógnita, no un valor numérico PLANTEAR el problema: Con base en los conceptos que haya elegido en el paso Identificar, seleccione las ecuaciones que usará para resolver el problema y decida cómo las usará. Si resulta apropiado, dibuje la situación descrita en el problema. . ¿Cómo resolver problemas en física?
EJECUTAR la solución: En este paso se hacen cálculos. Antes de enfrascarse en los cálculos, haga una lista de las cantidades conocidas y desconocidas, e indique cuál o cuáles son las incógnitas o las variables. Después, despeje las incógnitas de las ecuaciones. EVALUAR la respuesta: La meta de la resolución de problemas en física no es sólo obtener un número o una fórmula; es entender mejor. Ello implica examinar la respuesta para ver qué nos dice. En particular, pregúntese: “¿Es lógica esta respuesta?. . ¿Cómo resolver problemas en física?
7 Los prefijos son potencias de 10 que se anteponen a una unidad de medida para simplificar su expresión. Potencia Prefijo Abreviatura 10 −^12 pico p 10 −^9 nano n 10 −^6 micro μ 10 −^3 mili m 10 −^2 centi c 10 −^1 deci d 101 deca da 102 hecto h 103 kilo k 10 (^6) mega M 109 giga G 1012 tera T a) 5000 m = 5x 103 m = 5 km (^) b) 0. 007 m = 7x 10 −^3 m = 7 mm Sistema Inglés o británico : sus unidades fundamentales son lb, pie y s. Sistema C.G.S: sus unidades fundamentales son centímetro cm, Gramo (g) y segundo (s). Otros sistemas de unidades son
Prefijos
Algunas longitudes representativas en el Universo Un número está expresado en Notación Científica(NC) si tiene la forma : Exponente y es un número real entero Coeficiente y cumple con: 1 ≤ 𝐴 < 10 Ejemplo 1 .Usar prefijos en las siguientes cantidades: a) 5000 m; b) 0.007 m.
a) 0.0023 m
b) 7700000 kg
2. 3 × 10
− 3
m
7. 7 × 10
6
kg
Ejemplo 2. Expresar las siguientes cantidades en notación científica: a) 0.0023 m; b) 7700000 kg.
La consistencia dimensional consiste en la verificación de la homogeneidad en las unidades o dimensiones de los términos en una ecuación. La dimensión de una cantidad física es un símbolo que representa a cualquier unidad de medida que corresponda a dicha cantidad.
Si la ecuación A= B+ C representa una relación entre cantidades
físicas, entonces todos los términos deben tener las mismas dimensiones. Por ejemplo, no se puede realizar la suma 2 kg + 5 m.
3. Homogeneidad dimensional y conversión de unidades Dimension de cantidades físicas en el SI Cantidad Dimensión Longitud L Masa M Tiempo T Coriente eléctrica I Temperatura absoluta Θ Cantidad de sustancia N Intensidad luminosa J Ejemplo 3. Si 𝑥 es una longitud y 𝑡 un tiempo ¿qué dimensiones deben tener las constantes en las siguientes ecuaciones para que dichas ecuaciones sean dimensionalmente correctas? : 𝑎) 𝑥 = 𝑘 𝑡; (^) b) 𝑥 = 𝑘 𝑡^2 ; c) 𝑥 = 𝑘 1 + 𝑘 2 𝑡^2. Solución En las partes a) y b) se despeja la constante 𝑘 de la ecuación y se determina su dimension a partir de las demás cantidades. En la parte c) cada termino en el lado izquierdo debe tener las mismas unidades que 𝑥, de modo que se debe divider la dimension de 𝑥 por la dimension del coeficiente de cada constante a) 𝑥 = 𝑘 𝑡 ⇒ 𝑘 =
= 𝐿𝑇−^1
b) 𝑥 = 𝑘 𝑡^2 ⟹ 𝑘 =
𝑡^2
𝑡^2
𝑇^2
= 𝐿𝑇−^2
c) 𝑘 1 =
= 𝐿𝑇−^1 ; 𝑘 2 =
𝑡^2
𝑇^2
= 𝐿𝑇−^2
10
4. Incertidumbre y cifras significativas
Las mediciones siempre tienen incertidumbre. Si medimos el espesor de la portada de un hipotético libro con una regla común, la medición sólo será confiable al milímetro más cercano, y el resultado será de 1 mm. Sería erróneo dar este resultado como
- 00 mm; dadas las limitaciones del instrumento de medición, no se sabría si el espesor real es de 1. 00 mm o 0. 85. Pero si se usa un micrómetro, que mide distancias de forma confiable al 0. 01 mm más cercano, el resultado será 0. 75 mm. La distinción entre estas dos mediciones radica en su incertidumbre. La medida con micrómetro tiene menor incertidumbre y es más exacta. La incertidumbre también se llama error , porque indica la máxima diferencia probable entre el valor medido y el real. La incertidumbre o el error de un valor medido depende de la técnica empleada. A menudo indicamos la exactitud de un valor medido (es decir qué tanto creemos que se acerca al valor real) escribiendo el número, el símbolo ± y un segundo número que indica la incertidumbre de la medición. Si el diámetro de una varilla de acero se da como 56. 47 mm ± 0. 02 mm, esto implica que es poco probable que el valor real sea menor que 56. 45 mm o mayor que
- 49 mm. En una notación abreviada de uso común, el número
- 6454 ( 21 ) significa 1. 6454 ± 0. 0021. También podemos expresar la exactitud en términos de un error fraccionario o porcentual. En este caso el error se expresa como un % del valor medio de la medida. Por ejemplo 48 ohms ± 10%, que es equivalente a 48 ohms ± 5 ohms, En muchos casos, no se da explícitamente la incertidumbre de un número, sino que se indica con el número de dígitos informativos, o cifras significativas , en el valor medido. Si indicamos el espesor de la portada de un libro como de 0. mm, que tiene 2 cifras significativas (CS). Con esto queremos decir que los dos primeros dígitos son correctos (el cero no se cuenta como CS), pero el tercero es incierto. El último dígito está en la posición de las centésimas, así que la incertidumbre sería de 0.01 mm. Dos valores con el mismo número de cifras significativas pueden tener diferente incertidumbre; una distancia dada como 13 km también tiene dos cifras significativas, pero la incertidumbre es de más o menos 1 km. Las cifras significativas en cualquier medida son los dígitos que se conocen con certeza más un dígito que es incierto. Reglas para contar las C.S de una medida: a) Los ceros al principio de un número no son significativos. b) Los ceros dentro de un número son significativos c) Los ceros al final de un número, después del punto decimal, son significativos. d) En el caso de enteros sin punto decimal, que terminan con uno o más ceros, los ceros podrían ser significativos o no. La ambigϋedad podría eliminarse empleando notación científica, de modo que las CS sean las del coeficiente.
Ejemplo 6****. ¿Cuántas CS hay en cada una de las cantidades siguientes?. 1) 0.0045 kg; 2) 4.07 m; 4. 22 × 104 ft Criterios de redondeo estandar a) Se cuentan los dígitos a preservar de izquierda a derecha. b) Si se elimina un número mayor que 5 (es decir 6 , 7 , 8 , 9 ), entonces ,se le suma un 1 al dígito de la izquierda. d) Si se elimina un número menor que 5 (es decir:4,3,2,1,0),entonces , no se afecta el de la izquierda. Redondeo Redondear es aproximar un número por otro de menos dígitos, con el objetivo de simplificar los cálculos. Ejemplo 7 .Redondear a 3 CS las siguientes cantidades:1) 4.5456 kg;
- 63.07 m; 4. 224 × 104 ft
- 010 m ⇒ 4
- 22 × 104 ft ⇒ 3
- 0 .0045kg ⇒ 2 c) Si se elimina un número igual a 5 , entonces se le suma un 1 al dígito de la izquierda si es impar,pero si es par se queda igual. Solución
- 𝟎 7 m ≈ 63. 1 m
- 2 𝟐 4 × 104 ft ≈ 4. 22 × 104 ft
- 5 𝟒 56 kg ≈ 4. 54 kg Solución
Suma gráfica de vectores
Método del polígono : se coloca el primer vector y se le coloca en su punta la cola del siguiente , hasta que queden sin unir solo la cola del primer vector y la punta del ultimo, el vector suma es el que va dirigido desde la cola del primero hasta la cola del ultimo. Fíjese que el orden de los sumandos no altera el resultado de la suma: ¨ propiedad asociativa¨.
Ejemplo del la suma de dos vectores
- Este método tiene la ventaja de que se pueden sumar cualquier cantidad de vectores. Método del paralelogramo : se construye un paralelogramo juntando las colas de los vectores y se obtiene el vector resultante trazando una línea recta que inicia en la unión de las colas y termina en la esquina opuesta.
- Se le llama método del triángulo cuando solo se suman dos vectores. Hasta el momento el resultado de ambos métodos sería de forma cualitaiva,para obtener un resultado cuantitativo se debe usar una escala de medida , una regla y un transportador de ángulos. ¡Cuidado! Magnitudes en la suma de vectores. Es un error común suponer que si C = A + B entonces la magnitud C debería ser igual a la magnitud A más la magnitud B. En general, tal conclusión es errónea. Ver a continuación, el cambio en la dirección de uno de los vectores, hace cambiar la magnitud de la suma de los vectores.
𝐂^ Ԧ = 𝐀 + 𝐁
𝐂^ Ԧ = 𝐀 + 𝐁
- 00 m
- 0 cm = 5. 00 m cm = Escala Ejemplo 8. Determinar la suma de los siguientes vectores por el método del polígono : A = 10.0m , al este y B = 20 .0m , 30 onoreste.Suponer que la equivalencia : Esacala: 1. 0 cm ≡ 5. 0 m. Longitud de R a escala es 5.82cm y el ángulo medido fue 𝜃 = 20. 1 𝑜. Magnitud real de R : 5.82 cm x 5.00m/cm= 29.1 m
𝑅 = 29. 1 m , 20. 1
𝑜
Noreste
- Equivalencia de la magnitud de A:
- 0 m
- 00 m cm = 2. 00 cm
- Equivalencia de la magnitude de B:
- 0 m
- 00 m cm = 5. 00 cm Solución
- Se trazan los vectores en la cuadrícula o papel, manteniendo la orientación. Luego se mide la longitud y ángulo del segmento que va desde la cola del vector A hasta la punta del vector B.
- Se multiplica la magnitud en cm del vector resultante por la escala, para llevarlo a su tamaño y unidades originales o reales.
- Se calcula la escala:
Ejemplo 9. Determinar la suma de los siguientes vectores por el
método del triángulo. A = 10.0m , 130
o
con el este (referencia
estándar) y B = 20 .0m , 30
o
con el este.
Triángulo 130 o
- 0 o
B
A
Dibujo preliminar
Por la ley de los cosenos se determina la magnitud
C
2
2
2
− 2 𝐴B cos 𝛾
C = 𝐴^2 + 𝐵^2 − 2 𝐴B cos 𝛾
C = 10. 0 2 + 20. 0 2 − 2 10. 0 20. 0 cos 80 o^ m = 20. 7 m
Por la ley de los senos se determina la dirección
sen 𝛽
sen 80 o
𝛽 = sen
− 1
o
C =?
C = 20. 7 m, 58
o
Finalmente:
Estos ángulos en verde son iguales a 180
o
o
50 o, así que el ángulo opuesto a C es 80 o
- 0 o
sen 𝛽 =
𝐵 sen 80
o
20. 0 m 𝑠en 80
o
20. 7 m
o
o
o
6.2. Suma analítica por el método de las componentes
Para aplicar este método, se deben expresar los vectores
en dos componentes, las cuales se obtienen proyectando
el vector en los dos ejes de coordenadas
Las componentes de un vector pueden ser
números positivos o negativos:
Vectores unitarios
Un vector unitario es un vector con magnitud 1 , sin
unidades. Su única finalidad consiste en direccionar, es
decir, describir una dirección en el espacio. Los vectores
unitarios ofrecen una notación cómoda para muchas
expresiones que incluyen componentes de vectores.
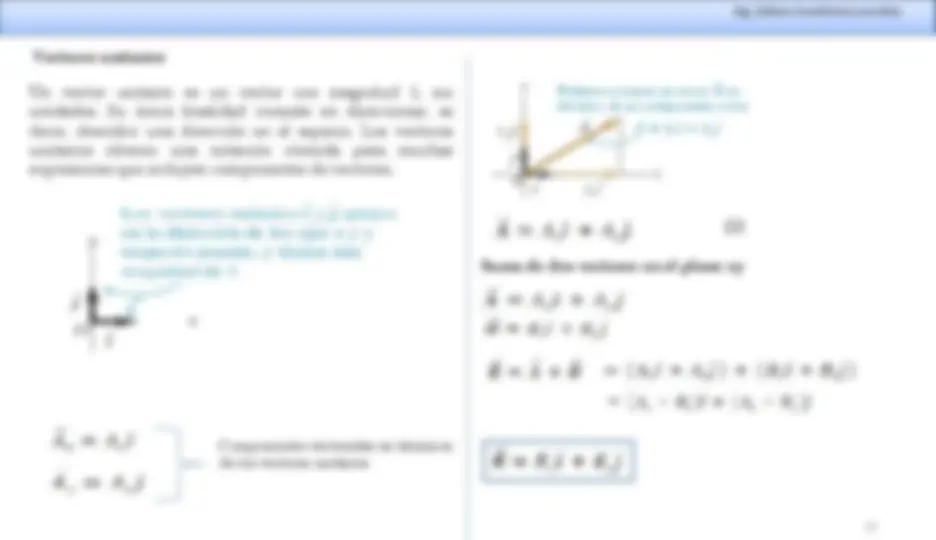
Componentes vectoriales en términos de los vectores unitarios
Suma de dos vectores en el plano xy
Ing. Edwin Garabitos Lara Msc.
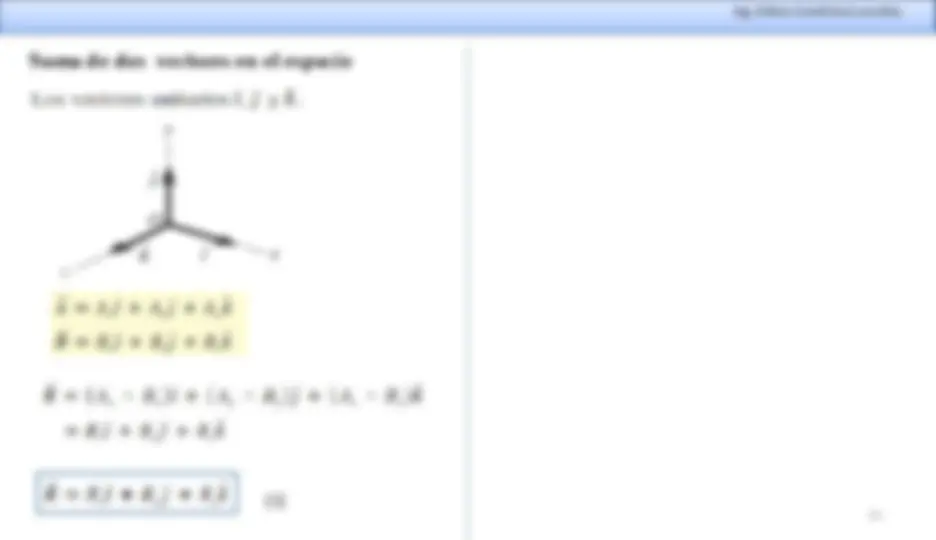
Suma de dos vectores en el espacio
Ing. Edwin Garabitos Lara Msc.
