Cálculo de Deflexión y Giro en Viga Elástica bajo Compresión, Diapositivas de Estructuras y Materiales

¡Descarga Cálculo de Deflexión y Giro en Viga Elástica bajo Compresión y más Diapositivas en PDF de Estructuras y Materiales solo en Docsity!

Unidad 3.

DEFLEXIONES EN VIGAS Y MARCOS.

Análisis Estructural

I.C. Gaspar H. Vela Martínez

Análisis Estructural

 Método del trabajo virtual

Adicionalmente

3.5 Método de área de momento.

3.6 Método de la viga conjugada.

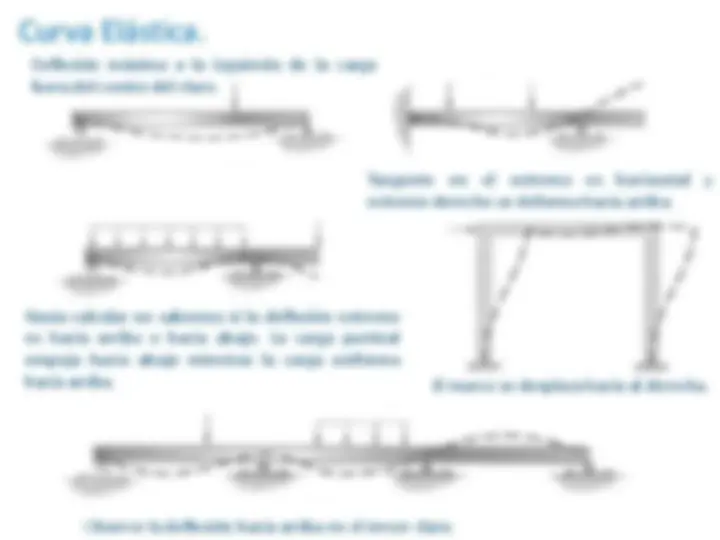
Curva Elástica.

Deflexión máxima a la izquierda de la carga fuera del centro del claro.

Tangente en el extremo es horizontal y extremo derecho se deforma hacia arriba.

Hasta calcular no sabemos si la deflexión extremo es hacia arriba o hacia abajo. La carga puntual empuja hacia abajo mientras la carga uniforma hacia arriba.

Observe la deflexión hacia arriba en el tercer claro.

El marco se desplaza hacia al derecha.

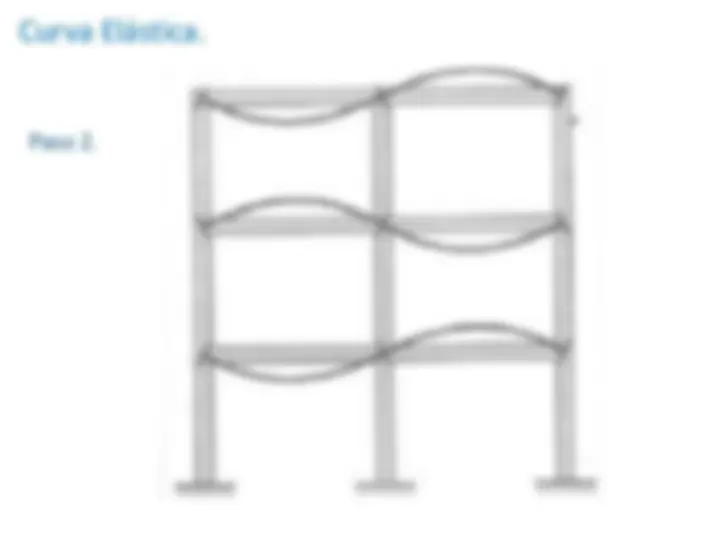
Curva Elástica.

Paso 1.

Paso 2.

Curva Elástica.

Paso 1.

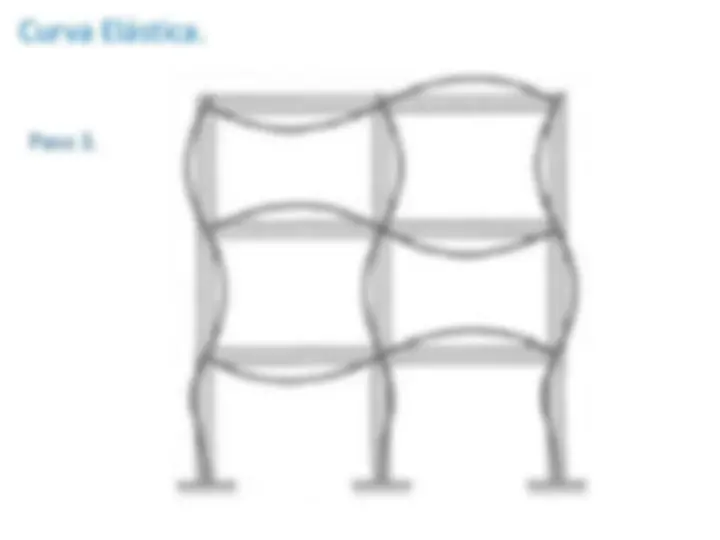
Curva Elástica.

Paso 2.

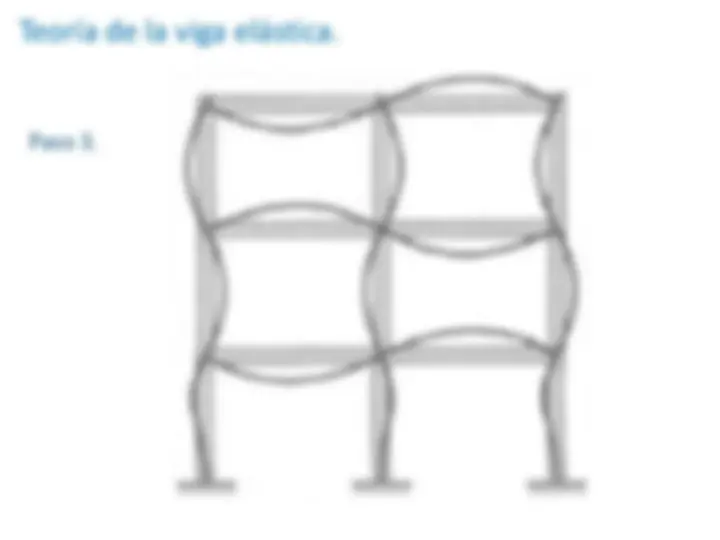
Teoría de la viga elástica.

Paso 3.

Si y

Sustituyendo tenemos:

Entonces:

La deformación del elemento causada por el momento flector M se mide por la curvatura de la superficie neutra. La curvatura se define como el inverso del radio de curvatura ρ.

Máxima Máximo

Teoría de la viga elástica. Curvatura.

donde dy / dx y d^2 y / dx^2 son la primera y segunda derivadas de la función y ( x ) representada por esa curva. Pero, en el caso de la curva elástica de una viga, la pendiente dy / dx es muy pequeña y su cuadrado es despreciable comparado con la unidad. Entonces:

Por lo que podemos decir:

Siendo: M= Ecuación del Momento como función de x

Si además, sabemos que la definición de curvatura es:

Teoría de la viga elástica.

Ecuación de la Viga de Bernoulli-Euler.

A partir de la ecuación anterior mediante integración podemos encontrar la pendiente ó giro (θ) y la deformación (δ ó y) de una viga.

Método de Integración.

Integrando

Integrando nuevamente

Si x=0, entonces y=0 y C 2 = Si x=L, entonces y=0 y

Entonces:

Determine la ecuación de la pendiente y deformación de las vigas. Establezca la ecuación y ubicación para la deformación máxima.

Ejercicios por el Método de Integración.

Sabemos que:

Entonces:

Método del área de momentos.

Primer teorema área-momento.

El cambio en la pendiente de la tangente de la curva elástica en cualquiera de dos puntos es igual al área bajo el diagrama de curvatura M/EI entre los puntos, con la condición de que la curva elástica sea continua entre los puntos.

Método del área de momentos.

Método del área de momentos.