




Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity

Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium


Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Prepara tus exámenes con los documentos que comparten otros estudiantes como tú en Docsity
Los mejores documentos en venta realizados por estudiantes que han terminado sus estudios
Estudia con lecciones y exámenes resueltos basados en los programas académicos de las mejores universidades
Responde a preguntas de exámenes reales y pon a prueba tu preparación

Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Comunidad
Pide ayuda a la comunidad y resuelve tus dudas de estudio
Descubre las mejores universidades de tu país según los usuarios de Docsity
Ebooks gratuitos
Descarga nuestras guías gratuitas sobre técnicas de estudio, métodos para controlar la ansiedad y consejos para la tesis preparadas por los tutores de Docsity
Ejercicio resuelto de problemas del libro de Analisis de Circuitos Electricos
Tipo: Ejercicios
1 / 5

Esta página no es visible en la vista previa
¡No te pierdas las partes importantes!




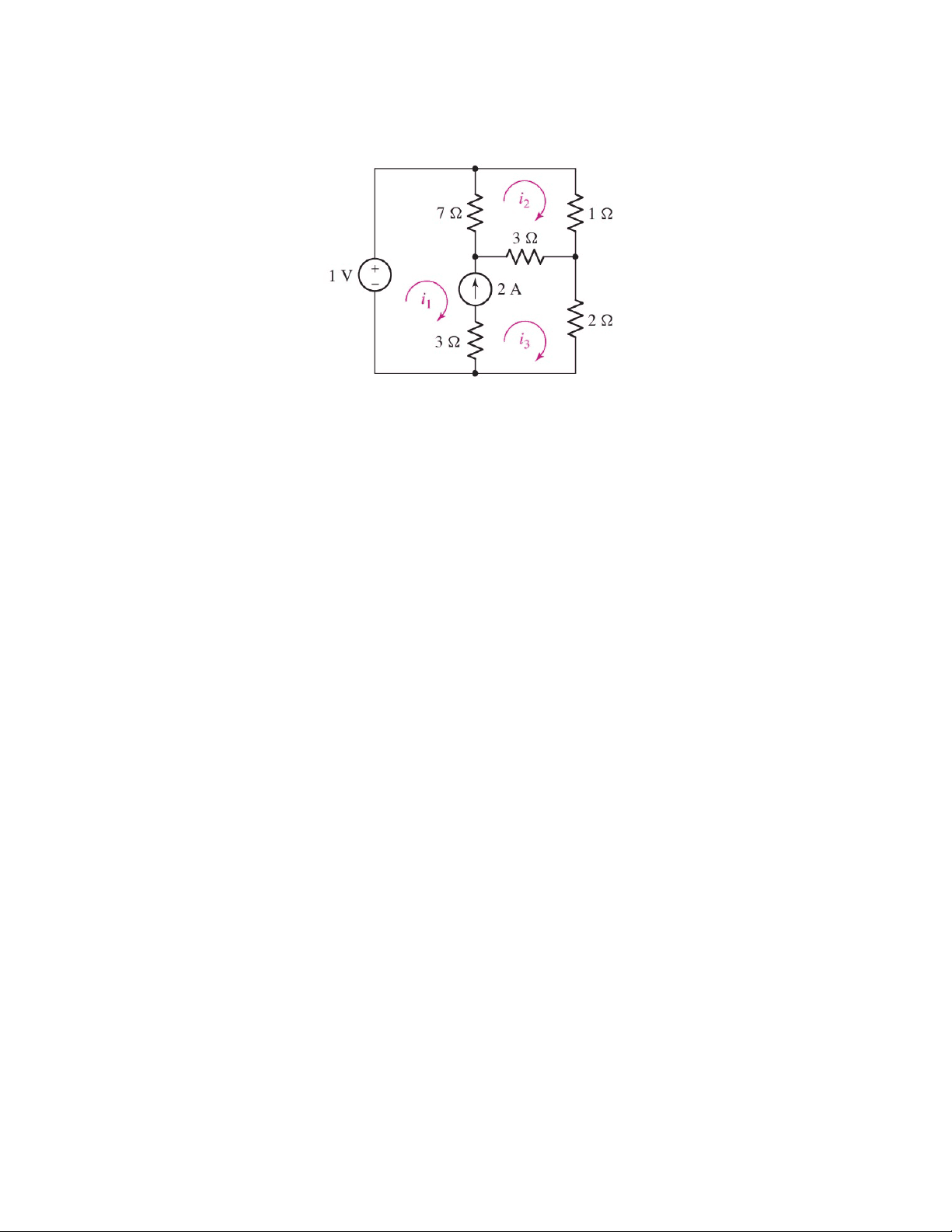
42. Determine los valores para las tres corrientes de malla de la figura 4..
Figura 4.67.
Analizando el circuito y colocando las incógnitas correspondientes usando la Ley
de Voltaje de Kirchhoff (LVK) obtenemos:
En la supermalla 1 y 3 :
− 1 + 7 ∙ ( i ¿¿ 1 − i 2
)+ 3 ∙ ( i ¿¿ 3 − i
2
)+ 2 i
3
− 1 + 7 i
1
− 7 i
2
3
− 3 i
2
3
7 i
1
− 7 i
2
− 3 i
2
3
3
7 i
1
− 1 0 i
2
3
En la malla 2 :
i
2
− i
1
2
¿
¿ 2 − i
3
7 i
2
− 7 i
1
2
2
− 3 i
3
− 7 i
1
2
− 3 i
3
Analizando la supermalla obtenemos:
i − i =− 2
( a )
( b )
( c )
Resolviendo las ecuaciones
( a ) ,
( b ) y
( c ) en función de
i
1
i
2
y
i
3
encontramos los
valores que le corresponden a las variables mencionadas, obteniendo:
7 i
1
− 10 i
2
3
− 7 i
1
2
− 3 i
3
i
1
− i
3
De la ecuación
( a ) y
( b ) haremos la eliminación de una de las 3 variables por el
método de reducción para hallar dos nuevas ecuaciones y así hallar 2 de las 3
incógnitas del ejercicio, seleccionando en nuestro caso la variable
i
2
, obteniendo:
7 i
1
− 10 i
2
3
− 7 i
1
2
− 3 i
3
Multiplicamos la ecuación ( a ) por
y la ecuación ( b ) por
para poder simplificar
y eliminar el valor de
i
2
, obteniendo ahora:
( 11 ) ∙ 7 i
1
−( 11 ) ∙ 10 i
2
3
77 i
1
− 110 i
2
3
−( 1 0 ) ∙ 7 i
1
+( 10 ) ∙ 11 i
2
−( 1 0 ) ∙ 3 i
3
− 7 0 i
1
2
− 30 i
3
Simplificando ambas ecuaciones obtenemos una nueva ecuación, por lo tanto:
77 i
1
− 110 i
2
3
− 70 i
1
2
− 30 i
3
7 i
1
3
Por lo que ahora obtenemos la siguiente ecuación:
7 i
( b )
( a )
( c )
( a )
( b )
( d )
i 3
= 782 m A
Lo último que nos resta es hallar el valor de
i
2
por lo que ahora sustituiremos los
dos valores encontrados en cualquiera de las 3 ecuaciones iniciales, al sustituirla
en
( a ) se obtiene:
7 i
1
− 10 i
2
3
7 ∙ (−1. 21875 )− 1 0 i
2
−8.53125− 10 i
2
− 1 0 i
2
− 1 0 i
2
i
2
i
2
i
2
=− 562 mA
Nuevamente, utilizando la herramienta llamada NI Multisim 14.0 verificamos que
los resultados hallados tanto de
i
1
como de
i
2
e
i
3
sean los correctos, obteniendo
enton-ces el siguiente circuito:
( a )