

















Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity

Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium


Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Prepara tus exámenes con los documentos que comparten otros estudiantes como tú en Docsity
Los mejores documentos en venta realizados por estudiantes que han terminado sus estudios
Estudia con lecciones y exámenes resueltos basados en los programas académicos de las mejores universidades
Responde a preguntas de exámenes reales y pon a prueba tu preparación

Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Comunidad
Pide ayuda a la comunidad y resuelve tus dudas de estudio
Descubre las mejores universidades de tu país según los usuarios de Docsity
Ebooks gratuitos
Descarga nuestras guías gratuitas sobre técnicas de estudio, métodos para controlar la ansiedad y consejos para la tesis preparadas por los tutores de Docsity
cinematica para estudiantes de ingenieria de sistemas y civil
Tipo: Resúmenes
1 / 24

Esta página no es visible en la vista previa
¡No te pierdas las partes importantes!

















ASIGNATURA: FÍSICA-I
DOCENTE RESPONSABLE: Ingº Rigoberto, HUAMAN HUALLPA.
Pucallpa, octubre del 2020
UNIVERSIDAD NACIONAL DE UCAYALI
FACULTAD DE INGENIERIA DE SISTEMAS Y DE
INGENIERIA CIVIL
ESCUELA PROFESIONAL DE INGENIERÍA CIVIL
encuentra en movimiento,
interpretamos que su posición esta
variando respecto a un punto
considerado fijo. El estudio de la
cinemática nos posibilita conocer y
predecir en que lugar se encontrara un
cuerpo, que velocidad tendrá al cabo de
cierto tiempo, o bien, en que lapso
llegara a su destino.
Hacer la descripción del movimiento de
un cuerpo significa precisar, a cada
instante, su posición en el espacio. Para
ello, debemos disponer de instrumentos
que nos posibiliten hacer mediciones,
como es el caso de las cintas métricas,
los relojes y las cámaras fotográficas
con luz estroboscópica; estas ultimas
permiten ver, aparentemente inmóviles o
con movimientos lentos, aquellos
cuerpos que tienen movimientos
rápidos, ya sean de rotación o
alternativos.
Estudiar el movimiento de un cuerpo quiere decir determinar su
posición en el espacio en función del tiempo, para ello se necesita un
sistema de referencia.
En el espacio euclidiano un sistema de queda definido por los
elementos siguientes.
a. un origen O, que es un punto del espacio físico.
b. una base vectorial del espacio vectorial asociado a dicho
espacio físico.
a un referencial si su posición con respecto a él cambia en el
transcurso del tiempo.
referencial, el cuerpo está en reposo en dicho referencial.
reposo de un cuerpo, vemos que ambos conceptos son relativos.
La posición de la partícula en
cualquier instante queda
definida por la coordenada x
medida a partir del origen O.
Si x es positiva la partícula se
localiza hacia la derecha de O y
si x es negativa se localiza a la
izquierda de O.
𝒎
𝒎
Si la partícula se mueve de P a P’ experimentando un
desplazamiento Δx positivo durante un intervalo de tiempo
Δt, entonces, la velocidad media será.
Si la función de una partícula en movimiento es: 𝑟Ԧ
(𝑡)
= (5𝑡Ԧ𝑖 − 𝑡
2
𝑗Ԧ)m, determine la
velocidad media para : 𝑡
𝑖
= 2𝑠 y 𝑡
𝑓
= 4𝑠
𝑟 Ԧ
(𝑓)
= ( 5 )( 4 )Ԧ𝑖 −(1)( 4 )
2
𝑗Ԧ = 20 𝑖Ԧ − 16 𝑗Ԧ
𝑟 Ԧ
(𝑖)
= ( 5 )( 2 )Ԧ𝑖 −(1)( 2 )
2
𝑗Ԧ = 10 Ԧ𝑖 − 4 𝑗Ԧ
∆ 𝑡 = 𝑡
𝑓
− 𝑡
𝑖
∆ 𝑟Ԧ = 𝑟Ԧ
(𝑓)
− 𝑟Ԧ
(𝑖)
∆ 𝑡 = 4 − 2 = 2 𝑠
𝑽
𝒎
=
( 10 Ԧ𝑖 − 12 𝑗Ԧ) m
2 s
= ( 5 Ԧ𝑖 − 6 𝑗Ԧ)
Τ 𝑚 𝑠
∆ 𝑟Ԧ = ( 10 𝑖Ԧ − 12 𝑗Ԧ) m
La rapidez media es el modulo de 𝑽
𝒎
𝑽
𝒎
= ( 5 𝑖Ԧ)
𝟐
+(− 6 𝑗Ԧ)
𝟐
= 𝟕, 𝟖𝟏
Τ 𝒎 𝒔
Ejemplo 01
Es la velocidad de la partícula en cualquier instante de tiempo se obtiene
llevando al límite la velocidad media es decir, se hace cada vez más
pequeño el intervalo de tiempo y por tanto valores más pequeños de x.
Por tanto:
0
0
lim( )
ˆ
lim( )
t
t
x dx
v
t dt
r dr dx
v i
t dt dt
Si una partícula se mueve de P a Q. A medida que Q se aproxima a P el
intervalo de tiempo tiende a cero tendiendo de esta manera las
pendientes a la tangente. Por tanto, la velocidad instantánea en P es
igual a la pendiente de la recta tangente en el punto P. La velocidad
instantánea puede ser positiva (punto P ), negativa (punto R ) o nula (punto
Q ) según se trace la pendiente correspondiente
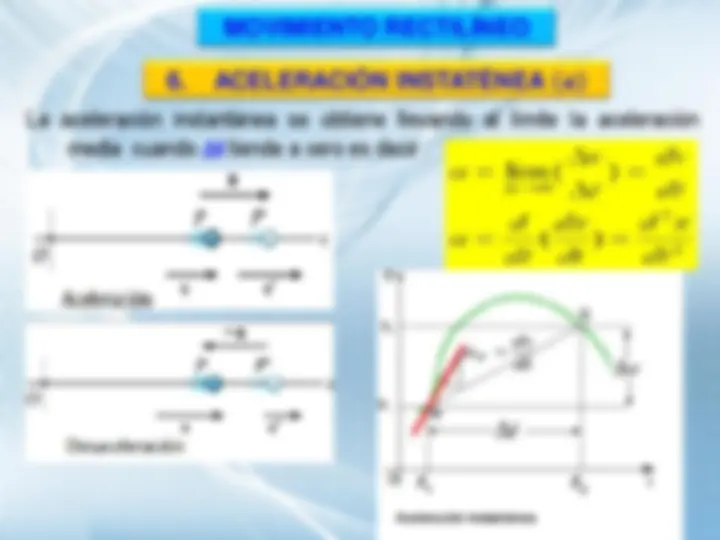
La aceleración instantánea se obtiene llevando al límite la aceleración
media cuando t tiende a cero es decir :
Ejemplo 02
Un jugador de baloncesto lanza la pelota con una velocidad de 𝑣
1
𝑚 𝑠, con tan mala suerte que rebota en el tablero con una
velocidad de 𝑣
2
Calcular la aceleración media sabiendo que el impacto contra el
tablero dura exactamente 0 , 02 s