Balanceo de lineas estudio del trabajo, Apuntes de Demografía Empresarial y Estudios Ambientales

¡Descarga Balanceo de lineas estudio del trabajo y más Apuntes en PDF de Demografía Empresarial y Estudios Ambientales solo en Docsity!

INSTITUTO TECNOLÓGICO DE

SAN JUAN DEL RÍO

INGENIERÍA INDUSTRIAL

ESTUDIO DEL TRABAJO II

TEMA: BALANCEO DE LÍNEAS

Área Académica de Ingeniería industrial

Resumen:

Con en este material el alumno explicará las características de los

sistemas de producción en línea y resolverá el problema de balanceo de

línea de producción; situación que se presenta en sistemas de fabricación

orientados al producto.

Tema:

BALANCEO DE LÍNEA

En los sistemas orientados al producto las máquinas o estaciones de trabajo

se agrupan de acuerdo a la secuencia de fabricación del producto. Lo que

se conoce como procesos en línea

Líneas de producción

Línea de fabricación

Línea de ensamble

Producción por línea

Actividades Simultáneas

Operaciones

Consecutivas

Flujo continuo Ritmo uniforme

Adyacentes

Operaciones equilibradas

Problema de balanceo de línea  (^) Consiste en distribuir físicamente las tareas en estaciones de trabajo con el objeto de balancear la carga de trabajo y disminuir el tiempo ocioso.

ESTACIÓN 1

T1, T

ESTACIÓN 2

T

ESTACIÓN 3

T4,T5, T

Planteamiento del problema

 Hay un conjunto de n tareas diferentes que deben efectuarse para

cada articulo.

 El tiempo requerido para terminarse la tarea i es una constante ti.

 El objetivo es organizar en grupos, ejecutándose cada grupo en una

sola estación de trabajo.

 En la mayoría de los casos, la cantidad de tiempo asignada a cada

estación de trabajo se conoce como antelación. Basándose en la tasa

deseada de producción de la línea de ensamble.

 Se conoce como el tiempo de ciclo y se denota como C.

formulación matemática

Sea t 1 , t 2 ,... , tn el tiempo requerido para terminar las respectivas

tareas. El contenido total del trabajo asociado con la producción de un

articulo, por ejemplo T, esta dado por

n

T = ∑ t i

i = 1

Formulación matemática

Para un tiempo dado de ciclo C, el numero posible de estaciones de

trabajo es [T / C ] donde los paréntesis rectangulares que indican el

T/C debe redondearse al siguiente entero.

Dificultades en el problema de balanceo

 Restricciones de precedencia: algunas tareas deben terminarse

según ciertas secuencias.

 Algunas tareas no pueden ejecutarse en la misma estación de

trabajo. (restricción de zonificación).

 Ciertas tareas podrían terminarse en la misma estación de

trabajo y otras podrían requerir más de un trabajador.

 (^) Es un problema combinatorio.

Diagrama de precedencia

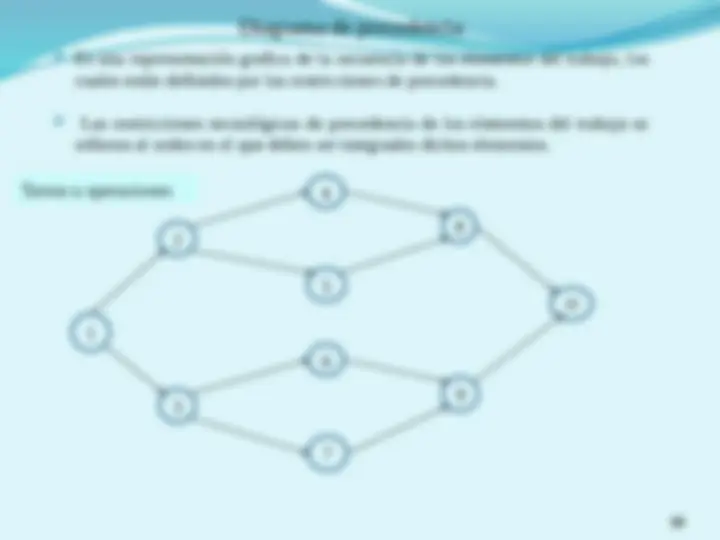
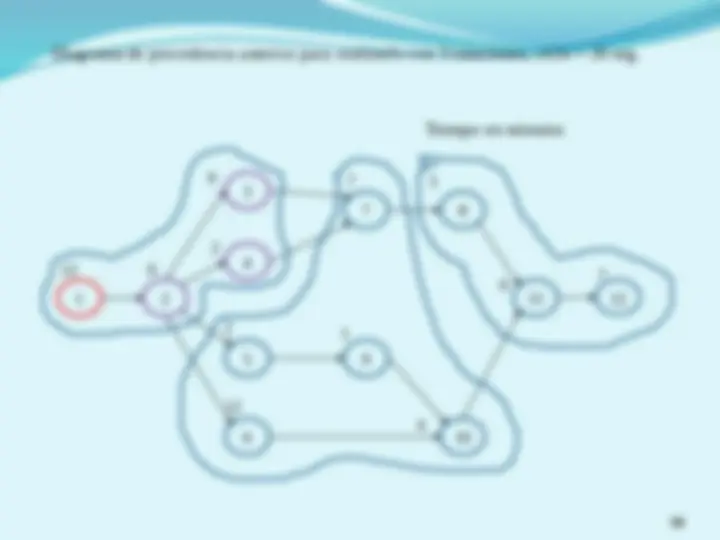
 (^) Es una representación grafica de la secuencia de los elementos del trabajo, los cuales están definidos por las restricciones de precedencia.  (^) Las restricciones tecnológicas de precedencia de los elementos del trabajo se refieren al orden en el que deben ser integrados dichos elementos. 1 2 3 4 5 6 7 8 9 10 Tareas u operaciones

Con diez estaciones (^) estaciones E1 E2 E3 E4 E5 E6 E7 E8 E9 E10 total 40 30 50 36 20 25 19 10 14 30 274 50 50 50 50 50 50 50 50 50 50 500 10 20 0 14 30 25 31 40 36 20 226 3 estaciones de trabajo 1 2 3 4 5 6 7 8 9 10 ESTACIÓN 1 ESTACIÓN 2 ESTACIÓN 3

Método de Kibridge & Wester

Considerar restricciones de precedencia entre las actividades, buscando

minimizar el numero de estaciones para un tiempo de ciclo dado

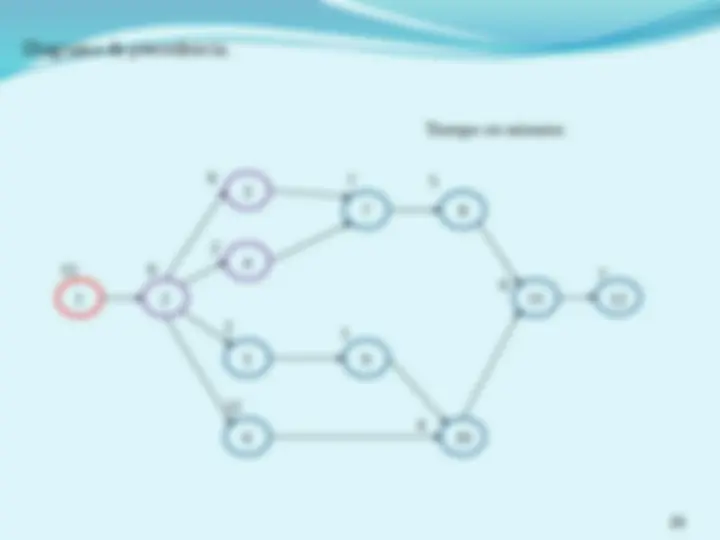
tarea tiempos precedencia 1 5 - 2 3 - 3 6 1 4 8 1, 2 5 10 3, 4 6 7 4 7 1 5, 6 8 5 7 9 3 7 total 48

El método se ilustra con el ejemplo siguiente

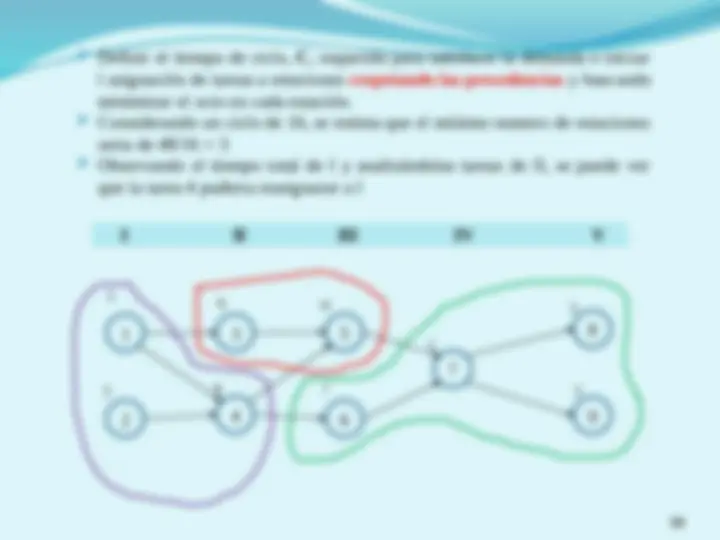
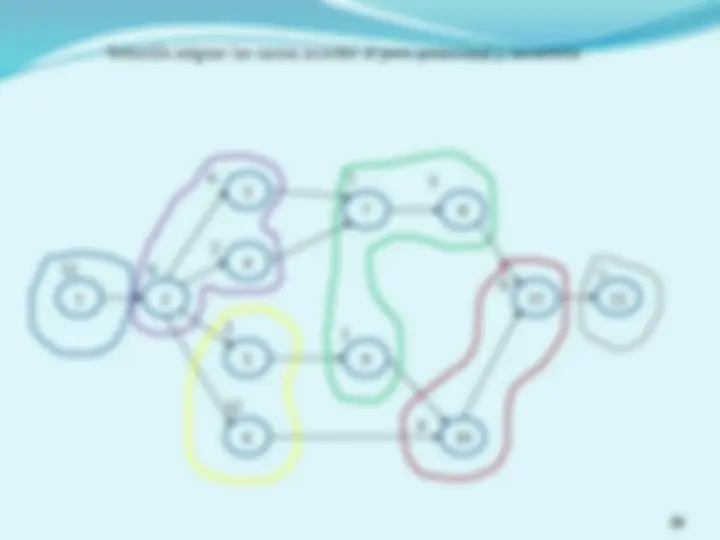
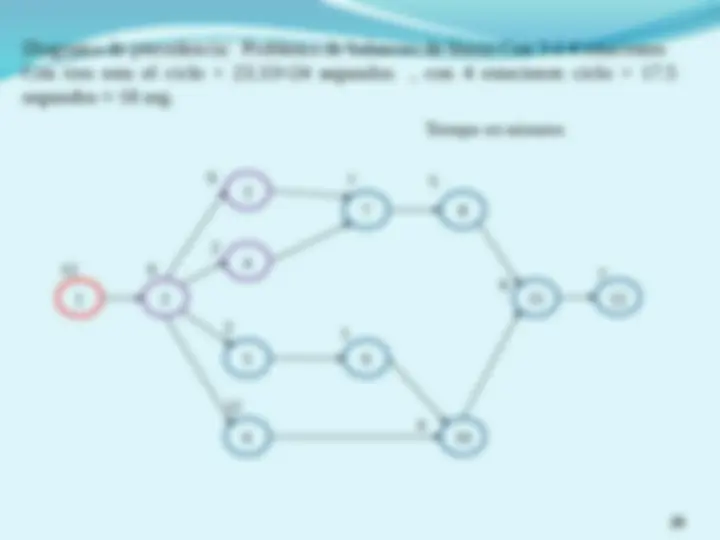
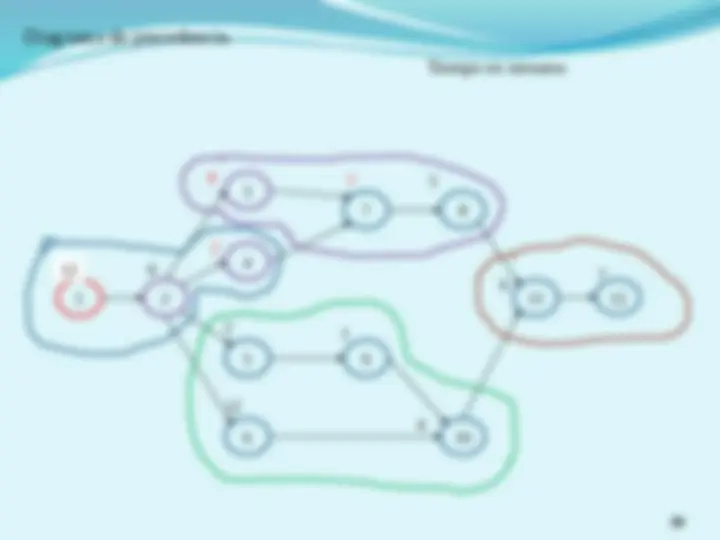
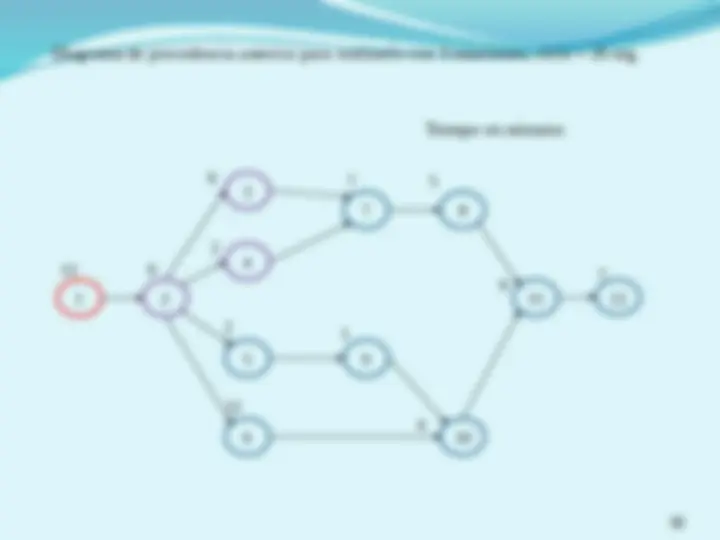
 (^) Definir el tiempo de ciclo, C , requerido para satisfacer la demanda e iniciar l asignación de tareas a estaciones respetando las precedencias y buscando minimizar el ocio en cada estación.  (^) Considerando un ciclo de 16, se estima que el mínimo numero de estaciones seria de 48/16 = 3  (^) Observando el tiempo total de I y analizándolas tareas de II, se puede ver que la tarea 4 pudiera reasignarse a I 1 2 3 4 5 6 7 8 9 I II III IV V 5 3 (^65) 8 10 7 1 3

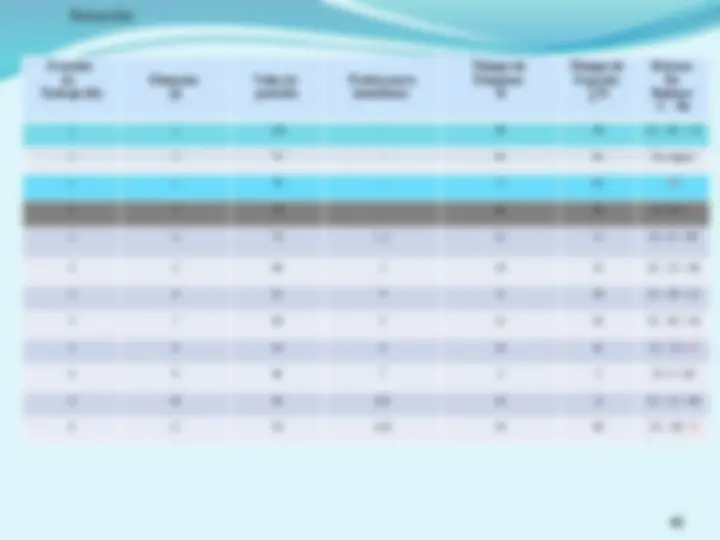
estación tareas tiempos Tiempo total Tiempo acumulado I 1,2,4 5,3,8 16 16 II 3,5 6,10 16 32 III 6,7,8,9 7 7 39 IV 7 7,1,5,3 1 40 V 8,9 5,3 8 48  (^) La línea se balanceo optimizando la cantidad de estaciones y con un ocio de cero estación tareas tiempos Tiempo total Tiempo acumulado I 1,2,4 5,3,8 16 16 II 3,5 6,10 16 32 III 6,7,8,9 7,1,5,3 16 48

PARÁMETROS PARA MODELAR EL SISTEMA DE LÍNEA DE ENSAMBLE Para entender mejor el problema de la línea de ensamble (así como los procedimientos de balanceo con ayuda de la computadora), es necesario definir el problema por medio de símbolos. Con este propósito se presentan. C = tiempo de ciclo K = numero de estaciones de trabajo 1 ≤ k ≤ K i = numero de identificación del elemento de trabajo 1≤ i ≤ N Ti = valor de tiempo para el elemento trabajo i. Sk = cantidad de tiempo asignado a la estación k Dk = retraso (tiempo ocioso) en la estación k D = retraso del balanceo en toda la línea de ensamble El tiempo ocioso del ciclo define el ritmo con el cual salen los productos ensamblados por el extremo de la línea de ensamble. Es también el máximo durante el producto que se ensambla progresivamente esta a disposición de una estación mientras pasa frente a ella. Dado un producto que se va a ensamblar sobre una línea transportadora. El tiempo de ciclo se puede determinar de esta manera

El retraso del balanceo en toda la línea (repartido entre todas las estaciones) se define mediante símbolos en la siguiente forma: K k D = ∑ dk = ∑ ( C – Sk) k = 1 k = 1 El ejemplo siguiente indica la relación entre d, c y s correspondiente a una sola estación Ejemplo: relación entre d, c y s. Para el tiempo de ciclo en particular el numero óptimo de estaciones es: K = ∑ Ti C Sk Dk = (C – Sk) 0 c C

n Eficiencia = ∑ Ti (100) i = 1 n * C n Retraso de la línea = ∑ C - Sk i = 1 Demora de balance = 100 (n*C - ∑ Ti) n * C El procedimiento de la técnica básica de calificación de ponderación de ubicación es como sigue: 1.- seleccionar la actividad con el mayor peso de ubicación y asignarla a la primera estación de trabajo. 2.- calcular el tiempo no asignado para la estación de trabajo calculando el tiempo acumulado para todas las actividades asignadas a la estación y restando esta suma de la duración del ciclo. 3.- seleccionar la actividad con el siguiente mayor peso de ubicación y tratar de asignarla a la estación de trabajo después de llevar a cabo las siguientes verificaciones:  (^) revisar la lista de actividades ya asignadas. Si las actividades inmediatamente predecesoras ya han sido asignadas, la precedencia no será violada; proceder al paso 3b. Si las actividades inmediatamente predecesoras no han asignadas proceder con el paso 4.