










































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
ega - ega - ega - ega
Typology: Exams
1 / 51

This page cannot be seen from the preview
Don't miss anything!












































Prepared by Dr. An Tran
in collaboration with Professor P. R. Heyliger
Department of Civil Engineering
Colorado State University
Fort Collins, Colorado
June 2003
Fundamentals of Linear
Vibrations
Developed as part of the Research Experiences of Undergraduates Program on
“Studies of Vibration and Sound” , sponsored by National Science Foundation
and
Army Research Office (Award # EEC-0241979). This support is gratefully
Fundamentals of Linear
Vibrations
A spring-mass system
General solution for any simple oscillator:
Governing equation of motion:
n
o o n^
2
n
(^2) o o
n n
n
o o o
ω
v ; C amplitude x 2
ω
T
1 f frequency(cycles/sec.or Hz)
; T periodof vibration T
2 naturalfrequency(rads/sec. ) m
k ω
x initialdisplacement; v initialvelocity x ; t time (sec.)
π
π
where:
Any simple oscillator
( )
( )
I
dt
d M
m x
dt
d F
Simple oscillator – Example 2
n
cg
2 2
2 ( k a ) a ml
M I o o
0
2 2 ml ka
, ω (unstable) l
a As
m
k , ω l
a Notelimits: When
n
n
0 0
1
Simple oscillator – Example 3
^
(^)
l
b
m
k ω
m ml m
ml
I I md
A l ml
I r dm x Adx
n
o cg
cg
l
3
12 2 3
12 12
2
2 2 2
2
(^32)
2 2 / 2
0
3
( )
2 ml k b b
M I o o
0
3
2
2
kb
ml
Equivalent springs
Springs in series:
same force - flexibilities add
Springs in parallel:
same displacement - stiffnesses add
1 2
k k k eq
k k k eq
P k k
( 1 2 )
1 2
f f P f P
P k k
eq
( )
1 1
1 2
1 2
1 2
1 2
f f f eq
Equivalent springs – Example 1
mx K x 0 eq
0
12 3
3 2
3 1
x
L
EI
L
EI m x
Equivalent springs – Example 3
0
2
2
ml mgl sin
Wl sin ml
M I o o
sin 0
l
g
l
g ω
l
g
n
We cannot define n +
since we have sin term
If < < 1, sin :
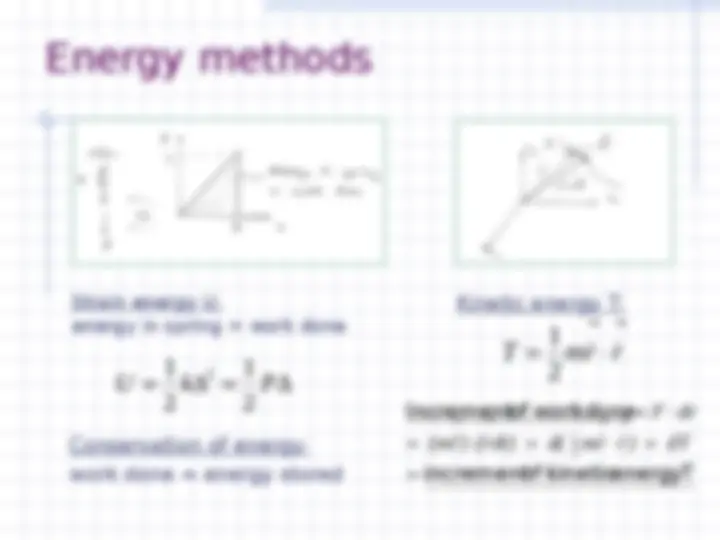
Energy methods
Strain energy U:
energy in spring = work done
Kinetic energy T:
Conservation of energy:
work done = energy stored
U k P 2
1
2
(^1 )
incrementofkineticenergy T
Incrementofwork done
(mr) (rdt) d( mr r) dT
F d r
2
1
Energy methods – Example
0
0
kxx mx x
(E ) dt
d
m x kx 0
2 2
2
2
2
1
2
1
2
1
2
1
E U T kx m x
T m x
U kx
Same as vector mechanics
Work-energy principles have many
uses, but one of the most useful is
to derive the equations of motion.
Conservation of energy: E = const.
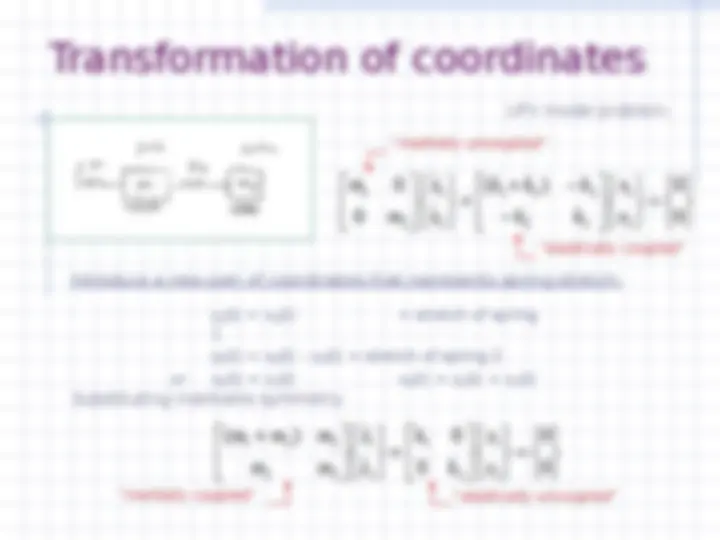
Two Degree-of-Freedom
Systems
Matrix form of governing equation
Special case: Undamped free vibrations
Examples
Inertially & elastically coupled/uncoupled
General approach: Modal equations
Example
Model equation
Special case: Undamped system
Undamped free vibrations
Zero damping matrix [C] and force vector {P}
cos( ) 2
1
2
1
t A
A
x
x
Assumed general solutions:
Characteristic polynomial (for det[ ]
=0):
0
1 2
(^212)
2
2
1
(^4 )
mm
k k
m
k
m
k k
2
1
1 2
1 2
2
2
2
1
1 2
2
2
1
(^212)
2
1 2
1
4
2
1
m m
k k
m
k
m
k k
m
k
m
k k
Eigenvalues (characteristic values):
Characteristic equation:
0
0
( )
( )
2
1 2 2 2 2
2
2 1 2 1
A
A
k k m
k k m k
Undamped free vibrations
Special case when k 1 =k 2 =k and m 1 =m 2 =m
Eigenvalues and frequencies:
fundamental period
fundamental frequency
ω
π T
m
k ω.
2
1 0618
m
k
618
3819 2 1
2 1
2
1
Two mode shapes (relative participation of each mass in the motion):
1
2 1. 618 2
1
(^2) k
k m
A
A 1 mode shape st 1
(^2)
k m
k
A
A 2 mode shape
nd
The two eigenvectors are orthogonal:
1 ( 1 ) 2
( 1 ) 1 A
A
1 ( 2 ) 2
( 2 ) 1 A
A Eigenvector (1) = (^) Eigenvector (2) =