Download Wind Engineering: Lift and Drag Forces on Airfoils and more Slides Environmental Law and Policy in PDF only on Docsity!

Wind Engineering

Recap

• In module 1.1, we looked at the course objectives, deliverables, and the t-square web site.
• In module 1.2, we looked at the history of wind turbine technology, some terminology, and definitions.
• In module 1.3, we looked at three studies – an off-shore site, guidelines for small wind turbines, and design of utility class wind turbines.
• Once module 1 is completed, you are ready to select a wind turbine anywhere in the world that you choose, and learn about the wind resources, energy needs, environmental issues, public policies, etc.

Use of Lift forces for Torque Production

L D

Vwind - Vinduced

L sin φ (^) Dcos φ Ω r

φ

Propulsive force = Lsinφ – Dcosφ

D Ωr

L Vwind^ Vinduced − ′ 

  ≅ ′^ −

Lift and Drag Forces

• In module 1.2, we discussed that the net thrust force is L’sin(φ) – D’ cos(φ) - L’ is the lift force per unit span of the rotor section, and D’ is the drag force per unit span.
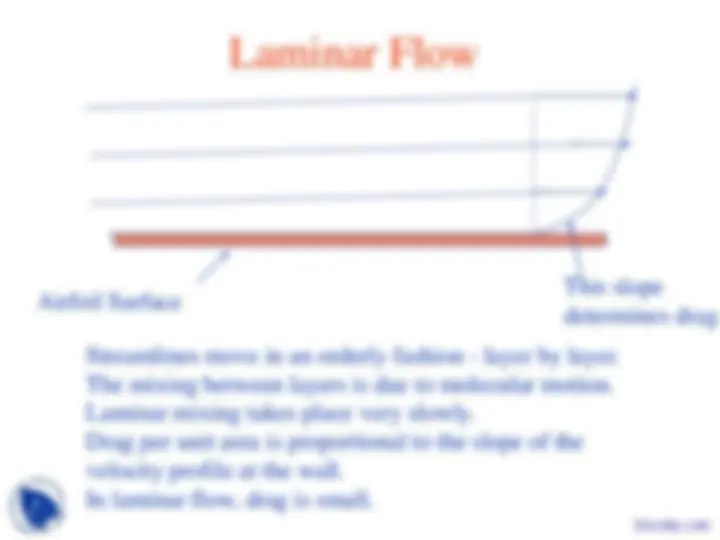
• In this module, we will learn how to compute or estimate Land D. - In module 3.1, we will first learn some basic characteristics of airfoils. - In module 3.2, we will develop the governing equations. - In module 3.3, we will show how to solve the equations on computer using panel method to compute lift. - In module 3.4, we will discuss how the panel method is used with empirical methods to compute the viscous drag forces - In module 3.5, we will discuss how designers change the shape of the airfoils to get high L’ and low D’ at the same time.

Uses of Airfoils

• Wings

• Propellers and Turbofans

• Helicopter Rotors

• Compressors and Turbines

• Hydrofoils (wing-like devices which can lift

up a boat above waterline)

• Wind Turbines

Evolution of Airfoils

Early Designs - Designers mistakenly believed that these airfoils with sharp leading edges will have low drag. In practice, they stalled quickly, and generated considerable drag.

An Airfoil is Defined as a

superposition of

• Chord Line

• Camber line drawn with respect to the chord

line.

• Thickness Distribution which is added to

the camber line, normal to the camber line.

• Symmetric airfoils have no camber.

Angle of Attack

α V∞

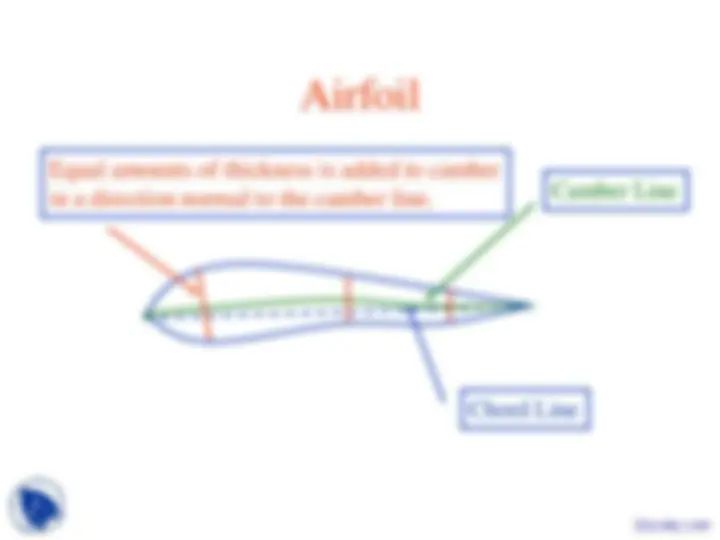
Angle of attack is defined as the angle between the freestream and the chord line. It is given the symbol α. Because modern wings have a built-in twist distribution, the angle of attack will change from root to tip. The root will, in general, have a high angle of attack. The tip will, in general, have a low (or even a negative) α.

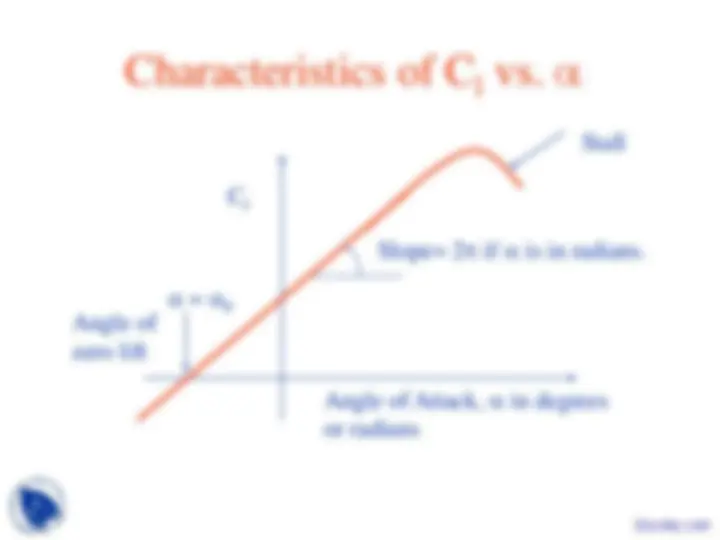
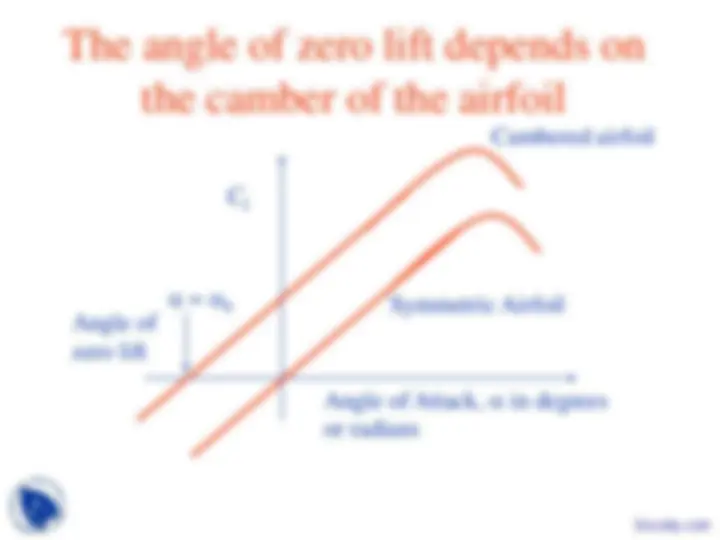
Sectional Lift and Drag Coefficients

• The sectional lift coefficient Cl is defined

as:

• Here c is the airfoil chord, i.e. distance

between the leading edge and trailing edge, measured along the chordline.

• The sectional drag force coefficient Cd is

likewise defined as:

V c

C L l (^) 2 2

1 ∞

′

ρ

V c

C D d (^) 2 2

1 ∞

′

ρ

Note that...

• When we are taking about an entire wing

we use L, D, C L and C D to denote the forces

and coefficients.

• When we are dealing with just a section of

the wing, we call the forces acting on that

section (per unit span) L´ and D ´, and the

coefficients Cl and C d

Pressure Forces acting on the

Airfoil

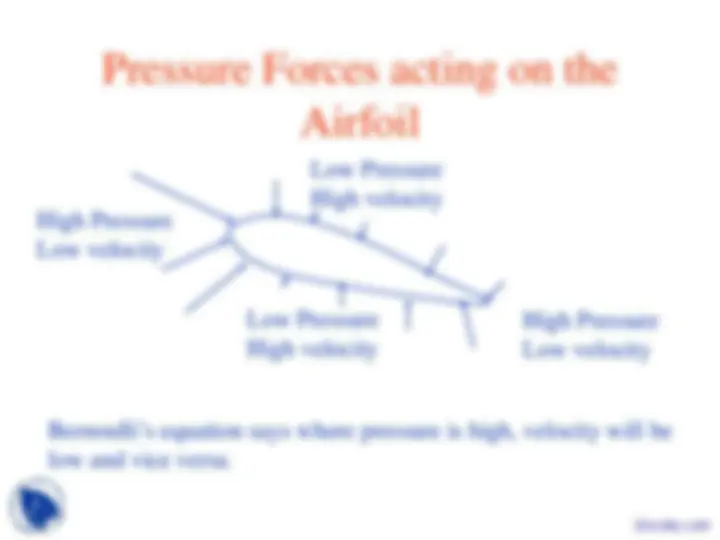
High Pressure Low velocity

High Pressure Low velocity

Low Pressure High velocity

Low Pressure High velocity

Bernoulli’s equation says where pressure is high, velocity will be low and vice versa.

Subtract off atmospheric Pressure p∞ everywhere. Resulting Pressure Forces acting on the Airfoil

High p-p (^) ∞ Low velocity

High p-p (^) ∞ Low velocity

Low p-p (^) ∞ High velocity

Low p-p (^) ∞ High velocity

The quantity p-p (^) ∞ is called the gauge pressure. It will be negative over portions of the airfoil, especially the upper surface. This is because velocity there is high and the pressures can fall below atmospheric pressure.

Relationship between L´ and p

(Continued)

∫([^ ]^ [^ ])

= − ∞ − − ∞

′= −

EdgeTrailing

EdgeLeading

lowerside upperside

EdgeTrailing

EdgeLeading

lowerside upperside

p p

p p

p p dx

L dx

Divide left and right sides by V^^2 c 2

1 ρ ∞



















 ′ = − − − ∞

∞ ∞

∞ ∞

Trailing Edge

EdgeLeading

lower upper c

d x V

p p V

p p V c

L 2 2 2 2

1 2

1 2

We get: (^1) ρ ρ ρ

Pressure Coefficient Cp

From the previous slide,



















 ′ = − − − ∞

∞ ∞

∞ ∞

Trailing Edge

EdgeLeading

lower upper c

d x V

p p V

p p V c

L 2 2 2 2

1 2

1 2

(^1) ρ ρ ρ

The left side was previously defined as the sectional lift coefficient C (^) l.

The pressure coefficient is defined as:

2 2

1 ∞

= − ∞ V

C p p p ρ

Thus, ( )

edgeTrailing

edgeLeading

Cl Cp , lower Cp , upper dcx