practical control engineering guide for engineers, managers, and practitioners (matlab example, Study Guides, Projects, Research of Control Systems

Download practical control engineering guide for engineers, managers, and practitioners (matlab example and more Study Guides, Projects, Research Control Systems in PDF only on Docsity!

Practical

C

: I__ 1- tro- _ _ 1- g11,.._ r~··l- ··n- ~~- ttl'

_ ____ .,

• (^) -

The McGraw· Hill Companies

Copyright ID 2009 by The McGraw-Hill Companies, Inc. All rights reserved Except as permitted under the United States Copyright Act of 1976. no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system. without the prior written permission of the publisher.

ISBN: 978-0-07-160614-

MHID. 0-07-160614-

The material in this eBook also appears in the print version of this title: ISBN· 978-0-07-160613-4. MHID: 0-07-160613-0.

All trademarks are trademarks of their respective owners Rather than put a trademark symbol after every occurrence of a trademarked name. we use names in an editorial fashion only. and to the benefit of the trademark owner. with no intention of infringement of the trademark. Where such designations appear in this book. they have been printed with initial caps.

McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions. or for use in corporate training programs. To contact a representative please visit the Contact Us page at www.mhprofessional.com.

Information contained in this work has been obtained by The McGraw-Hill Companies. Inc ("McGraw- Hill") from sources believed to be reliable. However. neither McGraw-Hill nor its authors guarantee the accuracy or completeness of any information published herein. and neither McGraw-Hill nor its authors shall be responsible for any errors. omissions. or damages arising out of use of this information This work is published with the understanding that McGraw-Hill and its authors are supplying information but are not attempting to render engineering or other professional services. If such services are required the assistance of an appropriate professional should be sought

TERMS OF USE

This is a copyrighted work and The McGraw-Hill Companies. Inc. ("McGraw-Hill") and its licensors reserve all rights in and to the work. Use of this work is subject to these terms. Except as permitted under the Copyright Act of 1976 and the right to store and retrieve one copy of the work. you may not decompile. disassemble, reverse engineer. reproduce, modify. create derivative works based upon. transmit. distribute. disseminate. sell. publish or sublicense the work or any part of it without McGraw-Hill's prior consent. You may use the work for your own noncommercial and personal use: any other use of the work is strictly pro- hibited. Your right to use the work may be terminated if you fail to comply with these terms.

THE WORK IS PROVIDED "AS IS." McGRAW-HILL AND ITS LICENSORS MAKE NO GUARAN- TEES OR WARRANTIES AS TO THE ACCURACY. ADEQUACY OR COMPLETENESS OF OR RESULTS TO BE OBTAINED FROM USING THE WORK, INCLUDING ANY INFORMATION THAT CAN BE ACCESSED THROUGH THE WORK VIA HYPERLINK OR OTHERWISE. AND EXPRESS- LY DISCLAIM ANY WARRANTY. EXPRESS OR IMPLIED. INCLUDING BUT NOT LIMITED TO IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. McGraw-Hill and its licensors do not warrant or guarantee that the functions contained in the work will meet your requirements or that its operation will be uninterrupted or error free. Neither McGraw-Hill nor its licensors shall be liable to you or anyone else for any inaccuracy. error or omission, regardless of cause. in the work or for any damages resulting therefrom McGraw-Hill has no responsibility for the content of any information accessed through the work. Under no circumstances shall McGraw-Hill and/or its licen- sors be liable for any indirect, incidental. special. punitive, consequential or similar damages that result from the use of or inability to use the work, even if any of them has been advised of the possibility of such damages. This limitation of liability shall apply to any claim or cause whatsoever whether such claim or cause arises in contract, tort or otherwise.

To Joshua Lucas, Ryan, Jennifel; Denise, Julie and Bertha and in memory of Wdda and Rudy.

Contents

Preface xvii

1 Qualitative ConceptsinControl Engineering and Process Analysis^.........^ •^ •^...............^1 1-1 What Is a Feedback Controller...........^1 1-2 What Is a Feedforward Controller^........^3 1-3 Process Disturbances...................^5 1-4 Comparing FeedforwardandFeedback Controllers............................^7 1-5 Combining FeedforwardandFeedback Controllers............................ 8 1-6 Why Is Feedback Control Difficult to Carry Out............................. 9 1-7 An Example of Controlling a Noisy Industrial Process....................... 10 1-8 What Is a Control Engineer^..............^15 1-9 Summary............................. 16

2 Introduction to Developing Control Algorithms^ •^17 2-1 Approaches to Developing Control Algorithms^............................^17 2-1-1 Style, Massive Intelligence, Luck, and^ Heroism (SMILH)^............^17 2-1-2 A Priori First Principles...........^18 2-1-3 A Common Sense, Pedestrian Approach.......................^19 2-2 Dealing with the Existing Process^........^19 2-2-1 What Is the Problem.............. 20 2-2-2 The Diamond Road^ Map^..........^20 2-3 Dealing with Control Algorithms Bundled with the Process.......................^27 2-4 Some General Comments about Debugging Control Algorithms.....................^29 2-6 Documentation and Indispensability...... 35 2-7 Summary.............................^36

3 Basic Concepts in Process Analysis.... •........ 37 3-1 The First-Order Process-an^ Introduction^37 3-2 Mathematical Descriptions of the First-Order Process^.....................^39

vii

Yiii Contents

3-2-1 The Continuous Tune Domain Model 39

3-2-2 Solution of the Continuous Tune

Domain Model 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 42

3-2-3 The First-Order Model and Proportional Control 0 0 0 0 0 0 0 0 0 0 0 0 0 44 3-2-4 The First-Order Model and

Proportional-Integral Control 0 0 0 0 0 0 48

3-3 The Laplace Transform 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 57 3-3-1 The Transfer Function and Block Diagram Algebra 00 00 00 00 00 00 00 00 0 59 3-3-2 Applying the New Tool to the First-Order Model 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 60 3-3-3 The Laplace Transform of Derivatives 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 61 3-3-4 Applying the Laplace Transform to the Case with Proportional plus Integral Control 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 62 3-3-5 More Block Diagram Algebra and Some

Useful Transfer Functions 0 0 0 0 0 0 0 0 0 65

3-3-6 Zeros and Poles 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 67 3-4 Summary o o o o 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 73

4 A New Domain and More Process Models 75

4-1 Onward to the Frequency Domain 0 0 0 0 0 0 0 0 75 4-1-1 Sinusoidally Disturbing the First-Order Process o o o o 0 0 0 0 0 0 0 0 0 0 0 75 4-1-2 A Little Mathematical Support

in the Tune Domain 00 00 00 00 00 0 00 0 79

4-1-3 A Little Mathematical Support in the Laplace Transform Domain 81 4-1-4 A Little Graphical Support 0 0 0 0 0 0 0 0 82 4-1-5 A Graphing Trick 00 00 00 00 00 00 00 00 85 4-2 How Can Sinusoids Help Us with Understanding Feedback Control? 87 4-3 The First-Order Process with Feedback Control in the Frequency Domain 0 0 0 0 0 0 0 0 91 4-3-1 What's This about the Integral? 0 0 0 0 94 4-3-2 What about Adding P to the I? 0 0 0 0 0 95 4-3-3 Partial Summary and a Rule of Thumb Using Phase Margin and Gain Margin 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 98

4-4 A Pure Dead-Tune Process o o o o 0 0 0 0 0 0 0 0 0 0 0 99

4-4-1 Proportional-Only Control of a Pure Dead-Tune Process 0 0 0 0 0 0 0 0 0 0 102 4-4-2 Integral-Only Control of a Pure Dead-Tune Process o o o 0 0 0 0 0 0 0 0 0 0 0 0 103

1 Contents

7 Distributed Processes......................... 177

7-1 The Tubular Energy Exchanger-

Steady State o o o o o o o o o o o o o o o o o o o o o o o o o o o o 177

7-2 The Tubular Energy Exchanger-Transient

Behavior o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o 180

7-2-1 Transfer by Diffusion o o o o o o o o o o o o o 182

7-3 Solution of the Tubular Heat Exchanger

Equation o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o 183

7-3-1 Inlet Temperature Transfer

Function o o o o o o o o o o o o o o o o o o o o o o o o o o o 184

7-3-2 Steam Jacket Temperature

Transfer Function o o 00 o 00 o 00 o 00 o 00 184

7-4 Response of Tubular Heat Exchanger to Step

in Jacket Temperature o o o o o o o o o o o o o o o o o o o 185

7-4-1 The Large-Diameter Case o o o o o o o o o 185

7-4-2 The Small-Diameter Case o o o o o o o o o 186

7-5 Studying the Tubular Energy Exchanger

in the Frequency Domain o o o o o o o o o o o o o o o o 188

7-6 Control of the Tubular Energy Exchanger o o 192

7-7 Lumping the Tubular Energy Exchanger o o 194

7-7-1 Modeling an Individual Lump o o o o o 194

7-7-2 Steady-State Solution o o o o o o o o o o o o o 196

7-7-3 Discretizing the Partial Differential

Equation o o o o o o o o o o o o o o o o o o o o o o o o 197

7-8 Lumping and Axial Transport o o o o o o o o o o o 200

7-9 State-Space Version of the Lumped Tubular

Exchanger o o o o o o o o o o o o o o o o o o o o o o o o o o o o o 202

7-10 Summary o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o 204

8 Stochastic Process Disturbances and the

Discrete Time Domain...................... •. 205

8-1 The Discrete Trme Domain o o o o o o o o o o o o o o 205

8-2 White Noise and Sample Estimates

of Population Measures o o o o o o o o o o o o o o o o o 206

8-2-1 The Sample Average o o o o o o o o o o o o o o 207

8-2-2 The Sample Variance o o o o o o o o o o o o o 207

8-2-3 The Histogram 00 00 00 00 00 00 00 00 00 208

8-2-4 The Sample Autocorrelation o o o o o o o 209

8-2-5 The Line Spectrum 00 00 00 00 00 00 00 o 212

8-2-6 The Cumulative Line Spectrum o o o o 212

8-3 Non-White Stochastic Sequences o o o o o o o o o 215

8-3-1 Positively Autoregressive

Sequences o o o o o o o o o o o o o o o o o o o o o o o 215

8-3-2 Negatively Autoregressive

Sequences o o o o o o o o o o o o o o o o o o o o o o o 218

Contents xi

8-3-3 Moving Average Stochastic Sequences....................... 220 8-3-4 Unstable Nonstationary Stochastic Sequences....................... 223 8-3-5 Multidimensional Stochastic Processes and the Covariance............... 225

8-4 Populations, Realizations, Samples, Estimates,

and Expected Values.................... 226 8-4-1 Realizations..................... 226 8-4-2 Expected Value.................. 227 8-4-3 Ergodicity and Stationarity........ 228

8-4-4 Applying the Expectation

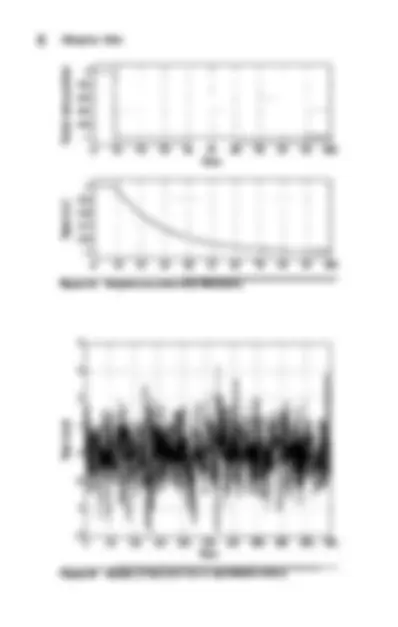
Operator........................ 228 8-5 Comments on Stochastic Disturbances and Difficulty of Control.................... 230 8-5-1 White Noise..................... 230 8-5-2 Colored Noise................... 231 8-6 Summary............................. 234

9 The Discrete Time Domain and the

Z-Transform • • • • • • • • • • • • • • •..... • • •.. •. • •. •. 235

9-1 Discretizing the First-Order Model 236 9-2 Moving to the Z-Domain via the Backshift Operator...................... 238 9-3 Sampling and Zero-Holding............. 239 9-4 Recognizing the First-Grder Model as a Discrete Trme Filter..................... 243 9-5 Descretizing the FOWDT Model.......... 244 9-6 The Proportional-Integral Control Equation in the Discrete Time Domain............. 244 9-7 Converting the Proportional-Integral Control Algorithm to Z-Transforms.............. 246 9-8 The PlfD Control Equation in the Discrete Trme Domain.......................... 247 9-9 Using the Laplace Transform to Design

Control Algorithms-the Q Method....... 249

9-9-1 Developing the Proportional-Integral Control Algorithm................ 249 9-9-2 Developing a PID-Like Control Algorithm....................... 252 9-10 Using the Z-Transform to Design Control Algorithms............................ 253 9-11 Designing a Control Algorithm for a Dead-Trme Process................. 256 9-12 Moving to the Frequency Domain........ 259

Contents xii

10-6-3 Finding the Open-Loop Eigenvalues and Placing the Closed-Loop Eigenvalues.................... 306 10-6-4 Implementing the Control Algorithm..................... 307 10-7 Proportional-Integral Control Applied to the Three-Tank Process.................. 310 10-8 Control of the Lumped Tubular Energy Excll.anger............................. 310 10-9 Miscellaneous Issues.................... 315 10-9-1 Optimal Control................ 315 10-9-2 Continuous Time Domain Kalman Filter.......................... 315 10-10 Summa~ .............................. 316

11 A Review of Control Algorithms............... 317

11-1 The Strange Motel Shower Stall Control Problem........................ 317 11-2 Identifying the Strange Motel Shower Stall Control Approach as Integral Only........ 321 11-3 Proportional-Integral, Proportional-Only, and Proportional-Integral-Derivative Control.. 322 11-3-1 Proportional-Integral Control..... 322 11-3-2 Proportional-Only Control 324 11-3-3 Proportional-Integral-Derivative Control........................ 324 11-3-4 Modified Proportional-Integral- Derivative Control.............. 326 11-4 Cascade Control........................ 328 11-5 Control of White Noise--Conventional Feedback Control versus SPC............ 332 11-6 Control Choices........................ 335 11-7 Analysis and Design Tool Choices........ 337

A Rudimentary Calculus........................ 339

A-1 The Automobile Trip.................... 339 A-2 The Integral, Area, and Distance.......... 339 A-3 Approximation of the Integral........... 344 A-4 Integrals of Useful Functions............. 345 A-5 The Derivative, Rate of Change, and Acceleration....................... 346 A-6 Derivatives of Some Useful Functions..... 348 A-7 The Relation between the Derivative and the Integral........................ 349 A-8 Some Simple Rules of Differentiation...... 350 A-9 The Minimum/Maximum of a Function... 351

xi¥ Contents

xvi Contents

 - 9-12-1 The First-Order Process Model - 9-12-2 The Ripple - 9-12-3 Sampling and Replication - 9-13 Filters - 9-13-1 Autogressive Filters - 9-13-2 Moving Average Filters - 9-13-3 A Double-Pass Filter - 9-13-4 High-Pass Filters - 9-14 Frequency Domain Filtering - 9-15 The Discrete Trme State-Space Equation - Experimental Data 9-16 Determining Model Parameters from - 9-16-1 First-Order Models - 9-16-2 Third-Order Models - 9-16-3 A Practical Method - Noise mputs 9-17 Process Identification with White 

• 9-18 Summary
• 10 Estimating the State and Using It for Control - Kalman Filter 10-1 An Elementary Presentation of the - 10-1-1 The Process Model - Postmeasurement Equations 10-1-2 The Premeasurement and - 10-1-3 The Scalar Case - 10-1-4 A Two-Dimensional Example - 10-1-5 The Propagation of the Covariances - 10-1-6 The Kalman Filter Gain - State 10-2 Estimating the Underdamped Process - Alternative Way to Find the Gain 10-3 The Dynamics of the Kalman Filter and an - Estimator 10-3-1 The Dynamics of a Predictor
  • 10-4 Using the Kalman Filter for Control - Integral Gain 10-4-1 A Little Detour to Find the
  • 10-5 Feeding Back the State for Control - 10-5-1 Integral Control - 10-5-2 Duals
  • 10-6 Integral and Multidimensional Control - Posing the Control Problem 10-6-1 Setting Up the Example Process and - Version 10-6-2 Developing the Discrete Trme - A-10 A Useful Test Function - A-ll Summary
  • B Complex Numbers • • • • - B-1 Complex Conjugates - B-2 Complex Numbers as Vectors or Phasors - 8-3 Euler's Equation - 8-4 An Application to a Problem in Chapter - 8-5 The Full Monty - 8-6 Summary
  • C Spectral Analysis • • • • • • • - Transform as a Data-Fitting Problem C-1 An Elementary Discussion of the Fourier - C-2 Partial Summary - C-3 Detecting Periodic Components - C-4 The Line Spectrum - Fitting Equation C-5 The Exponential Form of the Least Squares - C-6 Periodicity in the Trme Domain - C-7 Sampling and Replication - Resolution via Padding C-8 Apparent Increased Frequency Domain - Transform C-9 The Variance and the Discrete Fourier - on. V~ability of the Power Spectrum C-10 Impact of Increased Frequency Resolution - C-11 Aliasmg - C-12 Summary
• D Infinite and Taylor's Series • • • • • • • - D-1 Summary - Differential Equations • • • • E Application of the Exponential Function to - E-1 First-Order Differential Equations - E-2 Partial Summary - Differential Equation E-3 Partial Solution of a Second-Order - E-4 Summary - F The Laplace Transform • • • • • • • - (or a Step Change) F-1 Laplace Transform of a Constant - Greater than Zero F-2 Laplace Transform of a Step at a Trme - F-3 Laplace Transform of a Delayed Quantity - G-9 Eigenvalues of Matrices - G-10 Eigenvalues of Transposes - G-11 More on Operators - G-12 The Cayley-Hamilton Theorem - G-13 Summary
• H Solving the State-Space Equation • • • • • • • • • • • • • • - Domain for a Constant Input H-1 Solving the State-Space Equation in the Time - Integrating Factor H-2 Solution of the State-Space Equation Using the - Transform. Domain H-3 Solving the State-Space Equation in the Laplace - H-4 The Discrete Time State-Space Equation - H-5 Summary
  • I The Z-'Ii'ansform. • • • • • • • • • • • • • • • • • • • • • • • • • • • • - Transform. of a Sampler 1-1 The Sampling Process and the Laplace - 1-2 The Zero-Order Hold - (Step Change) 1-3 Z-Transform of the Constant - 1-4 Z-Transform of the Exponential Function - 1-5 The Kronecker Delta and Its Z-Transform. - in the z-Plane 1-6 Some Complex Algebra and the Unit Circle - 1-7 A Partial Summary - from Laplace Tranforms with Holds 1-8 Developing Z-Transform. Transfer Functions - 1-9 Poles and Associated Trme Domain Terms - 1-10 Final Value Theorem - 1-11 Summary
• J A Brief Exposure to Matlab • • • • • • • • • • • • • • • • • • - Index • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Preface

Y

ou may be an engineering student, a practicing engineer work- ing with control engineers, or even a control engineer. But I am going to assume that you are a manager. Managers of control engineers sometimes have a difficult chal- lenge. Many companies promote top managerial prospects laterally into unfamiliar technical areas to broaden their outlook. A manager in this situation often will have several process control engineers reporting directly to her and she needs an appreciation for their craft. Alternatively, technical project managers frequently supervise the work of process control engineers on loan from a department specializing in the field. This book is designed to give these manag- ers insight into the work of the process control engineers working for them. It can also give the student of control engineering an alter- native and complementary perspective. Consider the following scenario. A sharp control engineer, who either works for you or is working on a project that you are managing, has just started an oral presentation about his sophisticated approach to solving a knotty control problem. What do you do? If you are a successful manager, you have clearly convinced (perhaps without foundation) many people of your technical competence so you can probably ride through this presentation without jeopardizing your managerial prestige. However, you will likely want to actually critique his presentation carefully. This could be a problem since, being a successful manager, you are juggling several technically diverse balls in the air and haven't the time to research the technological underpinnings of each. Furthermore, your formal educational background may not be in control engineering. The above-mentioned control engineer, embarking on his presentation, is probably quite competent but perhaps he has been somewhat enthralled by the elegance of his approach and has missed the forest for the trees (it certainly happened to me many times over the years). You should be able to ask some penetrating questions or make some key suggestions that will get him on track and make him (and you) more successful. Hopefully, you will pick up a few hints on the kind of questions to ask while reading this book.

xvii

About tile Author

David M. Koenig had a 27 year career in process control and analysis for Corning, Inc., retiring as an Engineering Associate. His education started at the University of Chicago in chemistry, leading to a PhD in chemical engineering at The Ohio State University. He resides in upstate New York where his main job is providing day care for his six month old grandson.

Preface xix

assign homework having the students reproduce or modify the figures containing simulation and control exercises. I will, upon request, sup- ply you with a set of Matlab scripts or m-files that will generate all the mathematically based figures in the book. Send me an e-mail and con- vince me you are not a student in a class using this book.

References There aren't any. That's a little blunt but I don't see you as a control theory scholar-for one thing, you don't have time. However, if you are a college-level engineering student then you already have an arsenal of supporting textbooks at your beck and call.

AThumbnail Sketch of the Book

The first chapter presents a brief qualitative introduction to many aspects of control engineering and process analysis. The emphasis is on insight rather than specific quantitative techniques. The second chapter continues the qualitative approach (but not for long). It will spend some serious time dealing with how the engineer should approach the control problem. It will suggest a lot of upfront time be spent on analyzing the process to be controlled. If the approaches advocated here are followed, your control engineer may be able to bypass up the development of a control algorithm altogether. Since the second chapter emphasized process analysis, the third chapter picks up on this theme and delves into the subject in detail. This chapter will be the first to use mathematics extensively. My basic approach here and throughout the book will be to develop most of the concepts carefully and slowly for simple first-order systems (to be defined later) since the math is so much friendlier. Extensions to more complicated systems will sometimes be done either inductively without proof or by demonstration or with support in the appendices. I think it is sufficient to fully understand the concepts when applied to first-order situations and then to merely feel comfortable about those concepts in other more sophisticated environments. The third chapter covers a wide range of subjects. It starts with an elementary but thorough mathematical time-domain description of the first-order process. This will require a little bit of calculus which is reviewed in Appendix A. The proportional and proportional- integral control algorithms will be applied to the first-order process and some simple mathematics will be used to study the system. We then will move directly to the s-domain via the Laplace transform (supported in Appendix F). This is an important subject for control engineers and can be a bit scary. It will be my challenge to present it logically, straightforwardly, and clearly.