




























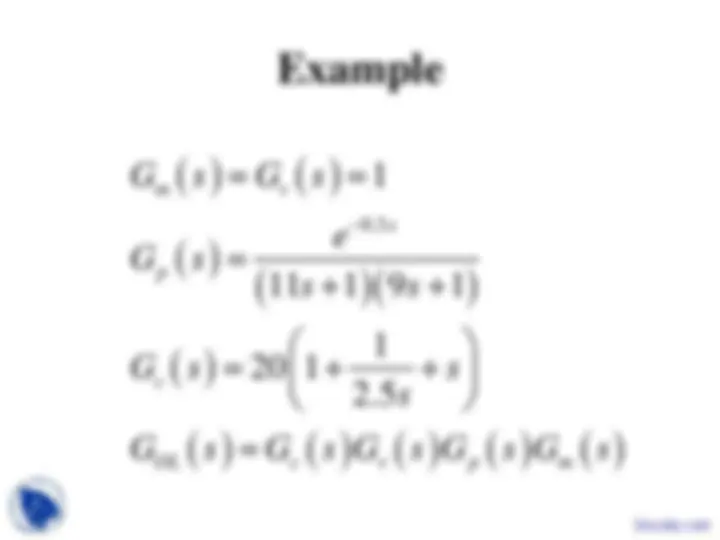











































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
This lecture is from Process Control course. Some key points for this lecture are: Frequency Response Analysis, Closed Loop Behavior, Closed Loop Stability, Good Disturbance, Set Point Tracking, Satisfactory, Degree of Robustness, Process Variations, Model Uncertainty, Low Sensitivity
Typology: Slides
1 / 82

This page cannot be seen from the preview
Don't miss anything!
































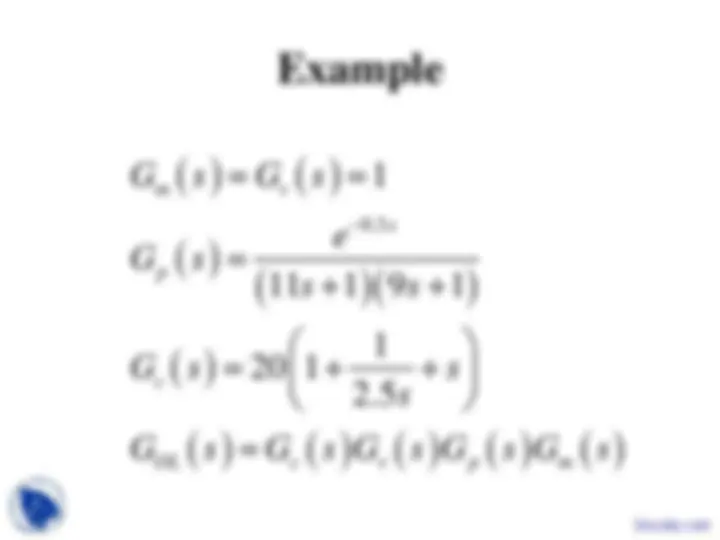










































Frequency response concepts and techniques play an important role in control system design and analysis.
In general, a feedback control system should satisfy the following design objectives:
Controller Design Using Frequency Response Criteria Advantages of FR Analysis:
( )
( ) ( )( ) ( )
( ) ( ) ( ) ( )
( )
1 2 1 1 2 1 1 2 1
π π
Dynamic Behavior of Closed- Loop Control Systems
(^) 4-20 mA
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
OL c v p m OL M c M v p m
( )
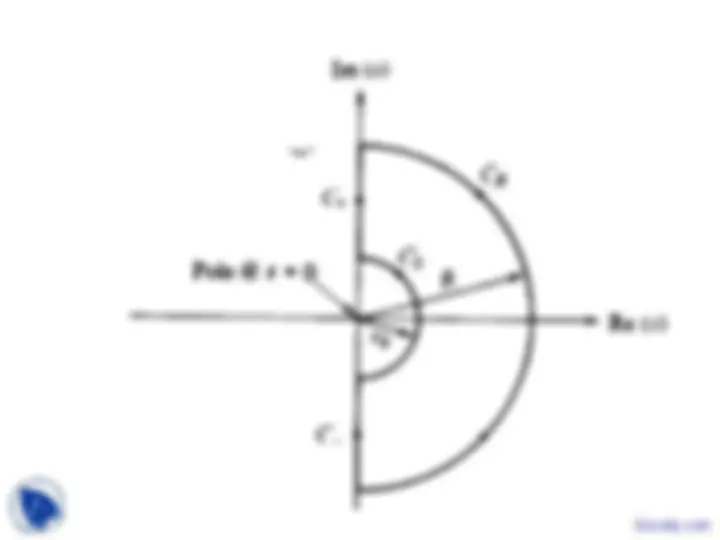
Nyquist Stability Criterion
( )
If is the number of times the Nyquist plot encircles the point ( 1, 0) in the complex plane in the clockwise direction, and is the number of open-loop poles of that lie
in the RHP, then
OL
N
P G s Z N P
−
= + ( )
is the number of unstable roots of 1 + GOL s = 0.
Example
3
3
/ 8 1 0
OL^ c
OL c
OL c OL OL OL
G s K s P
C s j G j K j G K G j G G j
=
∴ =
= = ∠ = → ∞ → ∠ → −
( )
( ) (^) ( ) ( ) ( )
( ) (^) ( ) ( ) ( ) ( ) (^) ( ) ( ) ( ) ( ) (^) ( ) ( ) ( )
3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
OL^ c s j c c
c cu c u
ω
ω
ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω
=
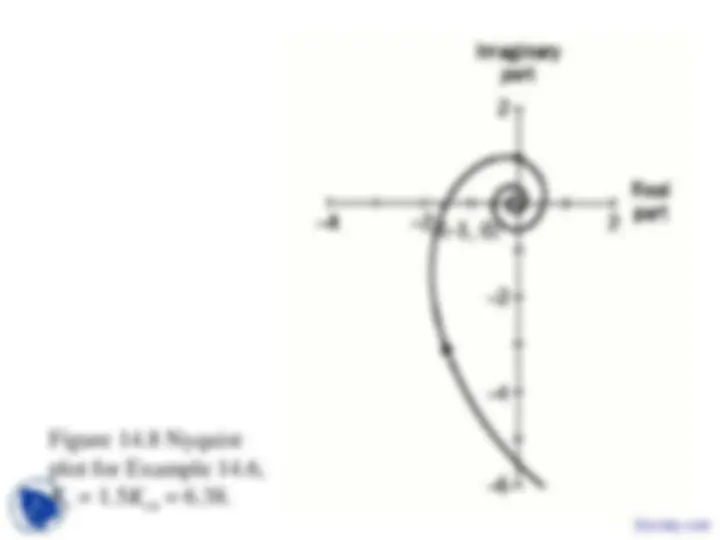
Example 2
( ) (^) ( )( )
( ) ( )
( ) ( ) ( )
( ) (^) ( )( )
2 (^2 2 2 2 2 )
2 2
1 5 1 0
(a) contour: (^1 5 ) (^1 5 6 1 5 36 1 5 )
(b) contour:
lim lim 1 5 1 lim 5 0
(c) contour: cojugate of.
OL^ c
OL c^ c c
R OL j^ j c^ j c j R R R
G s K P s s
C
G j K^ K j K j C G R e K^ K e R e R e R C C
φ φ φ φ
− →∞ →∞ →∞ − +
= (^) + + ⇒ =
= = − − − + (^) − + − +
⋅ = (^) ⋅ + ⋅ + ≈ →