





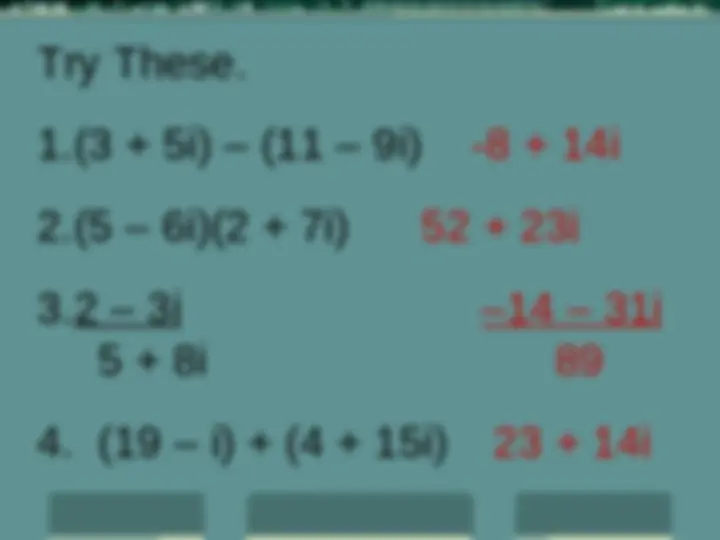


Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
An introduction to complex numbers, including their definition, representation in the form a + bi, and the rules for adding, subtracting, multiplying, and dividing complex numbers. It also includes examples and exercises for practice.
Typology: Assignments
1 / 11

This page cannot be seen from the preview
Don't miss anything!






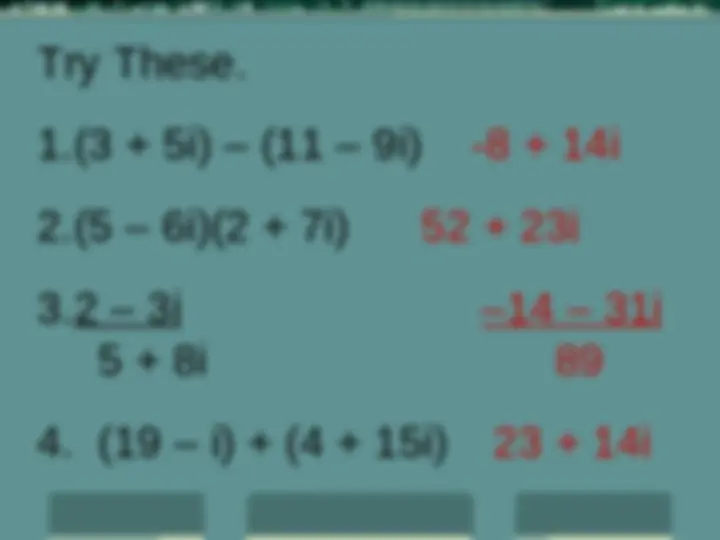
Introduction to Complex Numbers Introduction to Complex Numbers Adding, Subtracting, Multiplying And Dividing Complex Numbers SPI 3103.2.1 Describe any number in the complex number system.
Complex Numbers (a + bi) Natural (Counting) Numbers Whole Numbers Integers Rational Numbers Real Numbers Irrational #’s Imaginary #’s
When adding complex numbers, add the real parts together and add the imaginary parts together.
real part imaginary part
When subtracting complex numbers, be sure to distribute the subtraction sign; then add like parts.
To divide complex numbers, multiply the numerator and denominator by the complex conjugate of the complex number in the denominator of the fraction.
The complex conjugate of 3 – 5i is 3 + 5i.
2i 3 – 5i 21 + 35i + 6i + 10i 2 9 + 15i – 15i – 25i 2 21 + 41i – 10 9 + 25 (3 + 5i)
5i) 11 + 41i 34
Try These. 1.(3 + 5i) – (11 – 9i) -8 + 14i 2.(5 – 6i)(2 + 7i) 52 + 23i 3.2 – 3i –14 – 31i 5 + 8i 89
Investigate the powers of i. Power Exponential form simplified 1 i 0+i 2 i 2
3 4 5 6 7 8 9 12 27 70