




Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
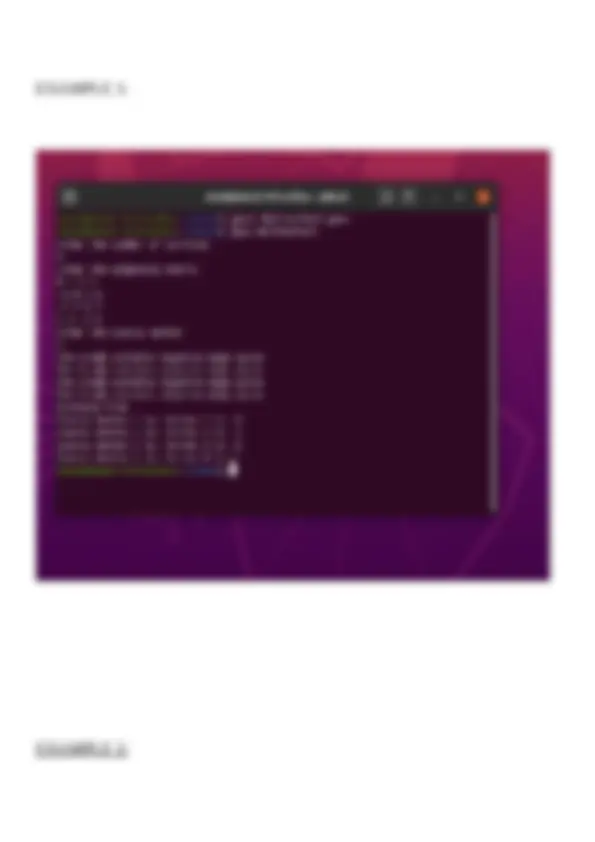
The document briefly explains the Bellman Ford algorithm along with the code in Java language. Output screenshots have also been attached for more reference
Typology: Assignments
1 / 6

This page cannot be seen from the preview
Don't miss anything!




Bellman Ford algorithm helps us find the shortest path from a vertex to all other vertices of a weighted graph. It works correctly when some of the edges of the directed graph G may have negative weight. When there are no cycles of negative weight, we can find the shortest path between source and destination. It is slower than Dijkstra’s Algorithm but more versatile as it is capable of handling some of the negative weight edges. Based on the ‘Principle of Relaxation’ in which more accurate values gradually recovered an approximation to the proper distance by until eventually reaching the optimal solution.
import java.util.Scanner; class BellmanFord { private int d[]; private int n; public static final int MAX_VALUE=999; public BellmanFord(int n) { this.n=n; d= new int[n+1]; } public void BellmanFordEval(int source,int a[][]) { for(int node=1;node<=n;node++) { d[node]=MAX_VALUE; } d[source]=0; for(int node=1;node<=n-1;node++) { for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(a[i][j]!=MAX_VALUE) {
n=sc.nextInt(); int a[][]=new int[n+1][n+1]; System.out.println("Enter the adjacency matrix"); for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { a[i][j]=sc.nextInt(); if(i==j) { a[i][j]=0; continue; } if(a[i][j]==0) { a[i][j]=MAX_VALUE; } } } System.out.println("Enter the source vertex"); source=sc.nextInt(); BellmanFord bellmanford=new BellmanFord(n); bellmanford.BellmanFordEval(source,a); sc.close(); } }