Mechanics of Materials: Stress and Strain under Axial Loading, Assignments of Mechanics

Download Mechanics of Materials: Stress and Strain under Axial Loading and more Assignments Mechanics in PDF only on Docsity!

Stress and Strain: Axial Loading

Nensi Lakrori, P.E., M.S., LEED AP BD+C

CIV E 301

MECHANICS OF MATERIALS

• Stress & Strain: Axial Loading
• Normal Strain
• Stress-Strain Test
• Stress-Strain Diagram: Ductile Materials
• Stress-Strain Diagram: Brittle Materials
• Hooke’s Law: Modulus of Elasticity
• Elastic vs. Plastic Behavior
• Fatigue
• Deformations Under Axial Loading
• Concept Application 2.
• Sample Problem 2.
• Static Indeterminate Problems
• Concept Application 2.
• Temperature Change

Contents

Stress & Strain: Axial Loading

• Suitability of a structure or machine may depend on the deformations in the structure as well as the stresses induced under loading. Statics analyses alone is not sufficient.
• Considering structures as deformable allows determination of

member forces and reactions which are statically indeterminate.

• Determination of the stress distribution within a member also requires consideration of deformations in the member.
• Chapter 2 is concerned with deformation of a structural member (bar, rod, plate) under axial loading. Later chapters will deal with torsional and pure bending loads.

Stress and Strain: Definitions

• STRAIN: Physical deformation

response of a material to stress

(think of strain as elongation of a

material).

• STRESS: Force per unit area that

results from an applied load.

Stress-Strain Test

Photo 2.2 Universal test machine used to test tensile specimens.

Photo 2.3 Elongated tensile test specimen having load P and deformed length L > L 0.

https://youtu.be/67fSwIjYJ-E

Stress-Strain Diagram: Ductile

Materials

Photo 2.4 Ductile material tested specimens: (a) with cross-section necking, (b) ruptured.

Fig. 2.6 Stress-strain diagrams of two typical ductile materials.

Cantilever vs. Simply Supported

http://neaco.co.uk/choosing-balconies /

https://www.quora.com/

A structure is a structure whether it's made of concrete or

steel, whether it's painted white or black.

Once the loads are applied

Internal loading is developed in the structural members

Structure Failure

The section and material should meet some criteria in the first place, such as:

• Avoiding failure of the structure : the capacity (tensile and bending strength) of the material (for a fixed section) should exceed the developed internal loads (axial and bending loads).
• Limit the deflection, cracking, thermal expansion: which is related to mechanical properties of the material (for example, Young's Modulus is a measure of the stiffness of a material and involved directly in the deflection of a beam. The bigger Young's Modulus is, the less deflection created).

Stress-Strain Diagram: Brittle

Materials

Fig 2.7 Stress-strain diagram for a typical brittle material.

Photo 2.5 Ruptured brittle materials specimen.

Figure 1: Brittle Cracking of a Wide Flange Beam

Figure 2: Brittle Cracking of a FRC Beam.

Structure Failure: Beams

Hooke’s Law: Modulus of Elasticity

• Below the yield stress

Modulusof Elasticity

=YoungsModulusor

E

σ E ε

• Strength is affected by alloying, heat treating, and manufacturing process but stiffness (Modulus of Elasticity) is not. Fig 2.11 Stress-strain diagrams for iron and different grades of steel.

Fatigue

• Fatigue properties are shown on σ-N diagrams. If stress is high fewer cycles cause rupture.
• When the stress is reduced below the endurance limit , fatigue failures do not occur for any number of cycles.
• A member may fail due to fatigue at stress levels significantly below the ultimate strength if subjected to many loading cycles.

Fig. 2.16 Typical σ -n curves.

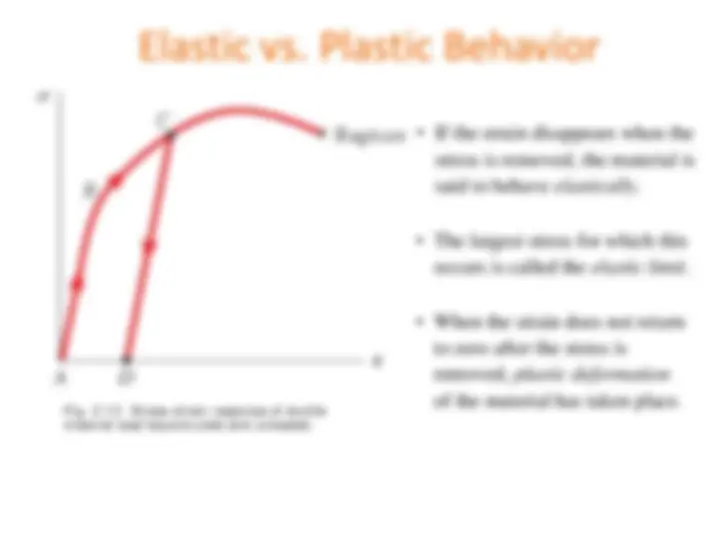
Deformations Under Axial Loading

AE

P

E

= E = =

σ σ ε ε

From Hooke’s Law:

From the definition of strain:

L

δ ε =

Equating and solving for the deformation,

AE

PL

With variations in loading, cross-section or material properties,

= ∑ i i i

i i A E

PL

Fig. 2.17 Undeformed and^ δ

deformed axially-loaded rod.