Download Assignment 1 - Data Structure and Algorithms and more Essays (university) Data Structures and Algorithms in PDF only on Docsity!
PROGRAM TITLE: HIGHER NATIONAL DIPLOMA IN COMPUTING
UNIT TITLE: DATA STRUCTURES & ALGORITHMS
ASSIGNMENT NUMBER: 0 1
ASSIGNMENT NAME: ASSIGNMENT BKC
SUBMISSION DATE: March 9 , 2021
DATE RECEIVED: …………………………………………….
TUTORIAL LECTURER:
WORD COUNT: 4097
STUDENT NAME:
STUDENT ID:
MOBILE NUMBER:
Summative Feedback:
Internal verification:
Table of content
- INTRODUCTION.......................................................................................................................................................
- Table of content......................................................................................................................................................
- LO1: Examine abstract data types, concrete data structures, and algorithms.......................................................
- Create a design specification for the Queue data structures.........................................................................
- 1.1. About Abstract data type.........................................................................................................................
- 1.2. Advantages of abstract data type............................................................................................................
- 1.3. What is the Queue data structure............................................................................................................
- 1.4. Implementation of the queue data structure using Java.........................................................................
- Sorting algorithms.........................................................................................................................................
- 2.1. Selection sort..........................................................................................................................................
- 2.2. Insertion sort..........................................................................................................................................
- Comparison between Insertion sort and Selection sort...........................................................................
- Pathfinding algorithms..................................................................................................................................
- 4.1. Dijkstra’s shortest path algorithm..........................................................................................................
- 4.2. Kruskal’s algorithm.................................................................................................................................
- LO2: Specify abstract data types and algorithms in a formal notation.................................................................
- Using an imperative definition, specify the abstract data type for a software stack...................................
- 1.1. What is an abstract data type?..............................................................................................................
- 1.2. Characteristics of the Stack data structure as an abstract data type...................................................
- 1.3. How to use Stack?..................................................................................................................................
- Examine the advantages of encapsulation and information hiding when using an Abstract Data Type.....
- 2.1. What is encapsulation and information hiding.....................................................................................
- 2.2. What advantages does encapsulation and information hiding bring to Abstract Data Type................
- LO3: Implement complex data structures and algorithms...................................................................................
- Implementing ADT and algorithm in creating Grade management application using Java.........................
- 1.1. Description.............................................................................................................................................
- 1.2. Entities....................................................................................................................................................
- 1.3. Functions................................................................................................................................................
- 1.4. Demonstration.......................................................................................................................................
- Error handling................................................................................................................................................
- LO4: Assess the effectiveness of data structures and algorithms.........................................................................
- Asymptotic analysis in analyzing the effectiveness of an algorithm.............................................................
- 1.1. What is Asymptotic analysis?.................................................................................................................
- 1.2. Why do we use asymptotic analysis in analyzing algorithms' performance?........................................
- 1.3. The downside of asymptotic analysis.....................................................................................................
- The two ways to measure the efficiency of an algorithm.............................................................................
- 2.1. Time complexity.....................................................................................................................................
- The trade-off when specifying an ADT..........................................................................................................
- References.............................................................................................................................................................
Figure LO1.1.1: Queue data structure
Based on how the queue is constructed, we have four basics functions for a queue:
Front: Get the front item of the queue Rear: Get the last item of the queue Enqueue: Add an item to the queue Dequeue: Remove(pop) the first item of the queue using the FIFO order
1.4. Implementation of the queue data structure using Java
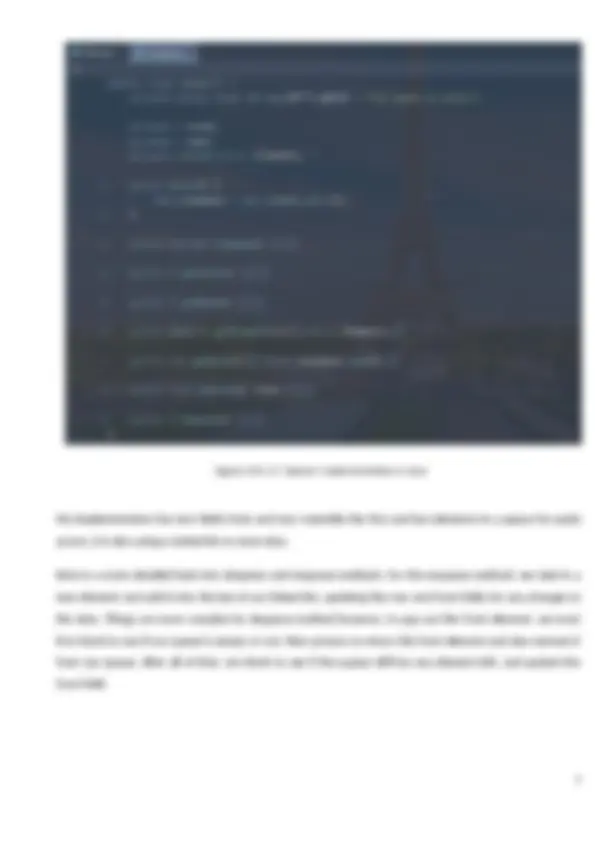
I have used Java code to create an abstract structure of a queue as follow
Figure LO1.1.2: Queue’s implementation in Java
My implementation has two fields front and rear resemble the first and last elements in a queue for quick access, it is also using a Linked list to store data.
Here is a more detailed look into dequeue and enqueue methods. For the enqueue method, we take in a new element and add it into the last of our linked list, updating the rear and front fields for any changes in the data. Things are more complex for dequeue method however, to pop out the front element, we must first check to see if our queue is empty or not, then process to return the front element and also remove it from our queue. After all of that, we check to see if the queue still has any element left, and update the front field.
Figure LO1.1.4: Testing the Queue
Figure LO1.1.5: The queue’s implementation’s test result
2. Sorting algorithms
2.1. Selection sort
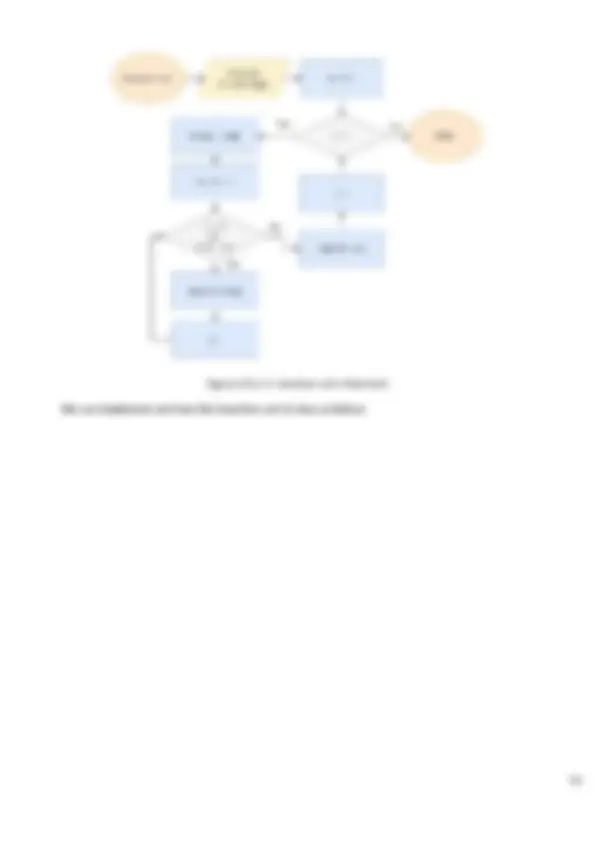
The selection sort sorts an array by finding the minimum value (if use ascending order) from the unsorted section of that array and putting it in the front.
Figure LO1.2.1: Selection sort’s flowchart Here is the implementation of this algorithm in Java code
Figure LO1.2.3: Selection sort’s test result
Time complexity:
Best-case: O(n^2 ) Average-case: O(n^2 ) Worst-case: O(n^2 )
Space complexity: O(1)
2.2. Insertion sort
The insertion sort is an easy algorithm. The basic idea of this algorithm is to divide an array into the sorted part and unsorted part, values from the unsorted part are picked, and inserted into the position they should be in the sorted part of that array
Figure LO1.2.4: Insertion sort idea
Here is this algorithm UML
Figure LO1.2.5: Insertion sort’s flowchart
We can implement and test the insertion sort in Java as below:
Space complexity: O(1)
3. Comparison between Insertion sort and Selection sort
Insertion sort Selection sort
Sorting by exchanging an element one at a time with a partially sorted array
Sorting by selecting the smallest element from the unsorted part of the array and exchanging it with the element in the correct location More efficient Less efficient
More complex More simple
Stable Not stable
Having O(n) best-case time complexity Make less swap compared to Insertion sort in the worst case
4. Pathfinding algorithms
4.1. Dijkstra’s shortest path algorithm
The Dijkstra algorithm is one of the basic algorithms used for pathfinding. The basic idea of this algorithm is as follow:
Step 1: Firstly, create a set to keep track of all paths from the source to every node, including the shortest path. Step 2: Assign a distance value to all paths in the input graph. Initialize all distances as INFINITE. Assign distance value as 0 for the starting point so that it is picked first. Step 3: Pick a node x next to the starting point , update the distance from x to every node next to it. Step 4: Repeat the 3rd^ step until there are no nodes that can go directly from starting point Step 5: Pick the node y from all the nodes you just found that has a minimum distance from the starting point Step 6: Repeat from 3rd^ step but with every node next to node y just founded Step 7: Update any distance that has a shorter path from the starting point
Here is an example:
Figure LO1.3.1: Dijkstra algorithm example
Take point A as the starting point, we can analyze that path as follow. The blueish word means that the node is chosen because it has the minimum value in that row:
Step A B C D E 1 - (∞,-) (∞,-) (∞,-) (∞,-) 2 - (4, A) (2, A) (∞,-) (∞,-) 3 - (4, A) ~ (6, C) (∞,-) 4 - ~ ~ (6, C) (7, B) 5 - ~ ~ ~ (7, B) 6 - ~ ~ ~ ~
As you can see, we take the shortest path from the starting point to a node after each node we analyze. The final result is that we have an empty set with every node having its own shortest path to go from the starting point (point A).
4.2. Kruskal’s algorithm
Kruskal’s algorithm is an algorithm used to find the minimum spanning tree of a connected graph.
Here are the steps of this algorithm:
Step 1: Sort all the edges in ascending order of their weight
LO 2 : Specify abstract data types and algorithms in a formal notation
1. Using an imperative definition, specify the abstract data type for a software stack.
1.1. What is an abstract data type?
An abstract data type is a type (a.k.a class in OOP) that does not have a specific implementation. Every abstract data type implementation can vary, however, they shall have the same signatures characteristics defined by it.
1.2. Characteristics of the Stack data structure as an abstract data type
The stack data structure is defined as a linear data structure that organizes its data in First In Last Out (FILO) or Last In First Out (LIFO) orders.
The stack has some basic methods: Push: Adds a new element into the stack, check for overflow if the stack is full Pop: Remove an item from the stack in the reverse order in which they are added (refer to FILO and LIFO order). Check for underflow if the stack is empty Peek (sometimes called Top): Get the top element of the stack And some less important methods based on different programming languages The stack shows its abstract characteristic by allowing any object with any data type can be added into its data, and that newly implemented stack will still have all methods above.
1.3. How to use Stack?
Most of the modern programming languages that support OOP have a built-in stack data structure, to use it, we usually just need to define a data type of its data. Here is how you do it in Java:
Figure II.1.1: Using stack data structure in Java Now we have an implemented stack that holds all integer values
All methods are the same no matter what the data type is
Figure II.1.2: Testing Stack’s implementations
2. Examine the advantages of encapsulation and information hiding when using an Abstract
Data Type.
2.1. What is encapsulation and information hiding
Encapsulation in programming means designing an object in a way that that object still can contain its necessary data(fields, methods) however, some unnecessary details will be restricted from access by an outside entity.
And by implementing good encapsulation theory in an object, we can achieve information hiding. So we can say encapsulation usually refers to information hiding.
2.2. What advantages does encapsulation and information hiding bring to Abstract Data Type
The main advantages of encapsulation are data security. It protects an object from unwanted access by unauthorized sources, allows access to a level without revealing the complex details below that level. Encapsulation also reduces human errors, simplifies the maintenance cost of a program, and overall makes your code easier to understand.
