Download Electric Circuit Terminology and Fundamentals: A Comprehensive Guide and more Study notes Analog Electronics in PDF only on Docsity!
Analog Electronics
1. Electric circuit terminology
− Voltage (SI unit: volts or V ) or electromotive force (emf): a measure of electrical field’s potential, analogous to potential energy in a gravitational field.
− Current (SI unit: ampere or A ): time rate of flow of charge where charge is measured in coulombs or C (𝐶 = 𝐴 ∙ 𝑠); that is, 𝐼(𝑡) = 𝑑𝑞 𝑑𝑡⁄ where I denotes current and q denotes quantity of charge.
− Direct current or DC : an electric current in which the flow of electric charge is only in one direction, i.e., unidirectional; Alternating current or AC : an electric current in which the flow of electric charge periodically reverses direction, usually sinusoidal.
− Impedance: Ohm’s law can be extended to the AC circuit analysis of resistor, capacitor, and inductor elements as 𝑉 = 𝑍𝐼, where Z is called impedance of the element. This is a complex number, and you can imagine Z as a complex, frequency-dependent resistance. The unit of
impedance is ohm (Ω). For the resistor, 𝑍𝑅 = 𝑅; for the capacitor, 𝑍𝐶 =^1 �^ 𝑗𝜔𝐶 ; for the inductor,
𝑍𝐿 = 𝑗𝜔𝐿.
Figure: Electric circuit terminology, where power source can be power supply, battery, or generator; a load consists of a network of circuit elements that may dissipate (lights or motors) or store electric energy (inductors or capacitors); the ground indicates a reference point in the circuit where the voltage is assumed to be zero (i.e., common ground).
2. Basic electrical elements
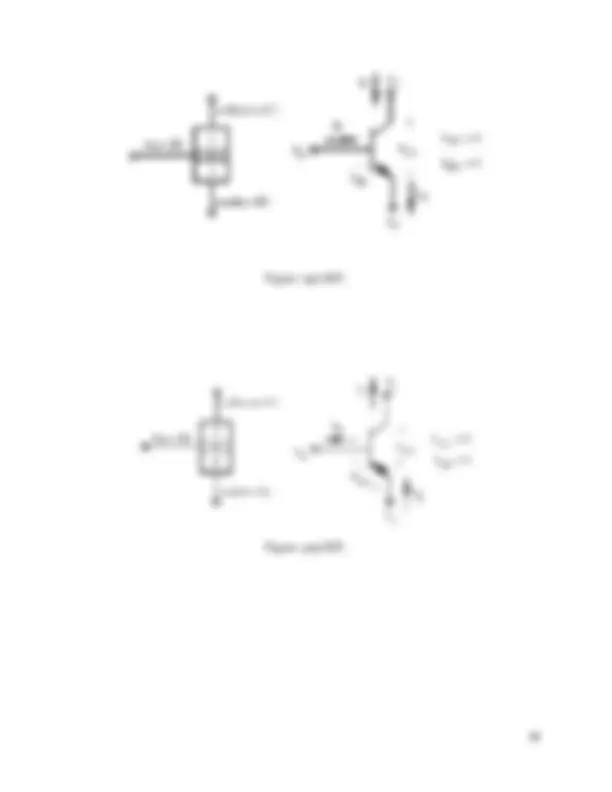
− Three basic passive electrical elements: resistor (R), capacitor (C), and inductor (L). Passive elements require no additional power supply, unlike active devices such as integrated circuits (IC; e.g., op-amps).
− Two types of ideal energy sources: voltage source ( V ) and current source ( I ). These ideal sources contain no internal resistance, inductance, or capacitance.
Figure: Schematic symbols for basic electrical elements.
Figure: Examples of basic circuit elements.
Figure: Resistor packaging.
− An axial-lead resistor’s value and tolerance are usually coded with four colored bands (a, b, c, tol), expressed as 𝑅 = 𝑎𝑏 × 10𝑐^ ± 𝑡𝑜𝑙𝑒𝑟𝑎𝑛𝑐𝑒 (%) ; precision resistors may have 4 digits: 𝑅 = 𝑎𝑏𝑐 × 10𝑑^ ± 𝑡𝑜𝑙𝑒𝑟𝑎𝑛𝑐𝑒 (%)
Figure: Axial-lead resistor color bands.
Table: Resistor color band codes
− Variable resistors, called potentiometer or pot or trim-pot , can provide a range of resistance values controlled by a mechanical screw, knob, or linear slide.
Figure: Potentiometer schematic symbols.
Notes: 1) A real resistor has a limited power dissipation capability designated in watts, and it may fail when this limit is exceeded. 2) Resistors come in a variety of shapes and sizes. As with many electrical components, the size of the device often has little to do with the characteristic value (e.g., resistance) of the device. Capacitors are one exception where a larger device usually implies a higher capacitance value. With most devices that carry continuous current, the physical size is usually related to the maximum current or power rating, both of which are related to the power dissipation capacities.
Capacitor: A passive element that stores energy in the form of an electric field. The field
is the result of a separation of electric charge. The simplest capacitor consists of a pair of parallel conducting plates separated by a dielectric material. The displacement of charge is called a displacement current because current appears to flow through the device as it charges or
discharge. The capacitor’s voltage-current relationship is defined as: 𝑉(𝑡) = 1 𝐶 ∫ 𝑖(𝜏)𝑑𝜏
𝑡 0 , where
Figure: RC charging circuit.
i) When capacitor is in charging:
1 𝐶 ∫ 𝑖
𝑡 0 (Kirchhoff’s voltage law or KVL) 𝑉𝑠 𝑠 =^ 𝑅𝐼
𝐶
𝐼(𝑠) 𝑠 (Laplace Transform)
𝑉𝑠 = 𝐼(𝑠) 1+𝑅𝐶𝑠 𝐶
𝐼(𝑠) = 𝑉𝑠 𝑅
1 𝑠+ (^) 𝑅𝐶^1
𝑉𝑠 𝑅 𝑒^
− (^) 𝑅𝐶^1 𝑡 (^) (Inverse Laplace Transform)
Notes : Kirchhoff’s voltage law or KVL: the sum of voltages around a closed loop or path is
zero, i.e., ∑ 𝑁𝑖=1 𝑉𝑖 = 0. In the above circuit, 𝑉𝑠 𝑅 is the maximum current;^ RC^ is the RC circuit time constant that is the time for the initial maximum current to decrease to be 36.8% (i.e., 𝑒 −1) of its maximum value, and is also the time required to charge the capacitor through the resistor to 63.2% (i.e., 1 − 𝑒 −1) of its fully charged voltage. The voltage across the capacitor is given as:
𝑡
0
1 𝑅𝐶𝑡^ 𝑑𝑡 =
𝑡
0
1 𝑅𝐶𝑡
Notes: 𝑉𝑠 is the maximum voltage that the capacitor can be charged.
ii) When the capacitor is in discharging, the battery has to be removed, and then we have:
Figure: RC discharging circuit.
𝑑𝑉𝑐 𝑑𝑡 +^
𝑉𝑐 𝑅 = 0^ (Kirchhoff’s current law or KCL)
𝐶𝑆𝑉𝑐(𝑠) +
1 𝑅 𝑉𝑐
𝑉𝑐( 0 ) 𝑠+ (^) 𝑅𝐶^1
𝑉𝑐(𝑡) = 𝑉𝑐(0)𝑒 −^
1 𝑅𝐶 𝑡
Notes: Kirchhoff’s current law or KCL: the sum of currents flowing into a closed node is zero, i.e., ∑^ 𝑁𝑖=1 𝐼𝑖 = 0. In the above circuit, 𝑉𝑐(0)^ is the maximum voltage of the capacitor prior to discharging.
iii) RC Filtering :
Figure: RC filtering.
Vout(s) Vin(s) =
1 Cs R+ (^) Cs^1
1 1+RCs (Transfer function in Laplace or s domain)
Vout(jω) Vin(jω) =^
1 1+jRCω (Sinusoidal Transfer Function; for LTI systems, just let^ 𝑠^ =^ 𝑗𝜔)
Figure: Examples of inductors.
The inductor’s characteristics are a direct result of Faraday’s law of induction given by:
𝑑𝜆 𝑑𝑡 (induced voltage depends on the rate of change of magnetic flux)
where 𝜆 is the total magnetic flux (measured in webers Wb) through the coil winding due to the current.
Figure: Inductor flux linkage. ( Note: the direction of flux follows right-hand rule, but the induced voltage depends on the rate of change of current; this figure shows the voltage polarity
when 𝑑𝑖(𝑡) 𝑑𝑡 > 0^ and the inductor works as a power load; when the current reach the maximum, the rate of change of current becomes zero and the induced voltage becomes zero, but the inductor has the maximum magnetic flux density B; when the power source is removed and inductor is going to work as a power source, the magnetic flux is decreasing and the polarity of the induced voltage changes; the addition of iron core could increase the flux density significantly)
For an ideal coil, the flux is proposal to the current
𝜆(𝑡) = 𝐿𝑖(𝑡) (Note: there is current, there is magnetic flux)
where L is the inductance (or self-inductance, measured in henry, H=Wb/A) of the coil, which is a measure of an inductor’s resistance to the change of current. The induced voltage across the inductor due to self-inductance is given by:
𝑑𝑖(𝑡) 𝑑𝑡 (Note that^
𝑑𝑖(𝑡) 𝑑𝑡 > 0^ or^
𝑑𝑖(𝑡) 𝑑𝑡 < 0; for constant current, self/back emf V ( t )=0)
Also
𝑡
0
We can see that the current through an inductor cannot change instantaneously because it is the integral of the induced voltage. It takes time to increase or decrease the current flowing through an inductor (be careful when you deal with motors or solenoids).
For solenoids:
𝜆 = 𝐿𝑖(𝑡) = 𝑁𝜙(𝑡)
where N is the number of turns of coils, 𝜙(𝑡)^ is the magnetic flux through one turn of coil, 𝜇 0 is
the magnetic constant, R is the radius of the coils, l is the length of solenoid, and 𝑛 = 𝑁 �𝑙 is the
number of turns per unit length.
Vs
R
L
Figure: RL charging/discharging circuit.
i) When the inductor is in charging:
𝑑𝑖(𝑡) 𝑑𝑡
Figure: Bode diagram for the RL filtering circuit when 𝑅 = 100𝛺 and 𝐿 = 10𝑚𝐻.
Notes: The above RL circuit is a high pass filter. The cut-off frequency for RL circuit is 𝜔𝑐 = 𝑅 𝐿.
3. Transformer
A transformer is a device used to change the relative amplitudes of voltage and current in an AC circuit. It consists of primary and secondary windings whose magnetic fluxes are linked by a ferromagnetic core.
Figure: Transformer.
The primary and secondary windings experience the same alternating magnetic flux. Therefore, the primary and secondary voltages (𝑉𝑃 and 𝑉𝑆) are related by:
𝑉𝑃 𝑁𝑃
where 𝑁𝑃 is the number of turns in the primary winding, 𝑁𝑆 is the number of turns in the secondary winding, and 𝜙 is the magnetic flux linked between the two coils. The secondary voltage is related to the primary voltage by:
where 𝑁 (^) 𝑆 𝑁 (^) 𝑃^ is the turns ratio of the transformer. If^ 𝑁𝑆^ >^ 𝑁𝑃, step-up transformer; if^ 𝑁𝑆^ <^ 𝑁𝑃, step- down transformer; if If 𝑁𝑆 = 𝑁𝑃, isolation transformer.
If we neglect losses in the transformer due to winding resistance and magnetic effects, the power in the primary and secondary circuits is equal:
𝐼𝑃 𝑉𝑃 = 𝐼𝑆 𝑉𝑆
Note: any DC component of voltage or current in a transformer primary winding will not appear in the secondary. Only alternating currents are transformed.
4. Voltage and Current Sources and Meters
− An ideal voltage source has zero output resistance (seen by the load) and can supply infinite current.
− An ideal current source has infinite output resistance and can supply infinite voltage.
− An ideal voltmeter has infinite input resistance (seen by the power source) and draws no current.
− An ideal ammeter has zero input resistance and no voltage drop across it.
Figure: Real voltmeter with input impedance.
5. Thevenin equivalent circuits
Sometimes, to simply the analysis of more complex circuits, we wish to replace voltage sources and resistor networks with an equivalent voltage source and series resistor. This is called a Thevenin equivalent of the circuit. Thevenin’s theorem states that, given a pair of terminals in a linear network (including DC resistance and AC impedance), the network may be replaced by an ideal voltage source 𝑉𝑂𝐶 in series with a resistance 𝑅 (^) 𝑇𝐻. 𝑉𝑂𝐶 is equal to the open circuit voltage across the terminals (can be measured), and 𝑅 (^) 𝑇𝐻 is the equivalent resistance across the terminals when independent voltage sources are shorted and independent current sources are replaced with open circuits.
Example:
Figure: Example illustrating Thevenin’s theorem.
Figure: Thevenin equivalent circuit.
6. Impedance matching
Often we must be careful when connecting different devices and circuits together. For example, when using certain function generators to drive a circuit, proper signal termination, or loading, may be required.
Figure: Signal termination.
Placing the 50Ω termination resistance in parallel with a higher impedance network helps match the receiving network input impedance to the function generator output impedance. This is
𝑉𝐿^2
(𝑅𝐿 + 𝑅𝑠)^2
𝑉𝑆^2
To find the load resistance that maximizes this power 𝑃𝐿, we set the derivative of the power equal to 0 and solve for the load resistance:
𝑑𝑃𝐿 𝑑𝑅𝐿
Solving for 𝑅𝐿 gives
𝑅𝐿 = 𝑅𝑆
The second derivative of power can be checked to verify that this solution results in a maximum and not a minimum. It shows that to maximize power transmission to a load, the load’s impedance should match the source impedance.
7. Semiconductor electronics
7.1 Introduction
− Conductors: Materials (like metals) have a large number of weakly bound electrons in what is called their conduction band. When an electric field is applied to a metal, the electrons migrate freely producing a current through the material. Because of the ease by which large currents can flow in these materials, they are called conductors.
− Insulators: Some other materials have atoms with valence electrons (for forming chemical bounds) that are tightly bound, and when an electric field is applied, the electrons do not move easily. These materials are called insulators.
− Semiconductors: A class of material (e.g., silicon or germanium), elements in group IV of the periodic table, have properties somewhere between conductors and insulators. They are called semiconductors.
− Holes : When a voltage is applied across a semiconductor, some of the valence electrons easily jump from the valence band to the conductance band and then move in the electric field to produce a current (although smaller than that which would be produced in a conductor). Its absence in the valence band is called a hole. A valence electron from a nearby atom can move to the hole, leaving another hole in its former place. This chain of events can continue, resulting in a current that can be thought of as the movement of holes in one direction or electrons in the other.
Figure: Valence and conduction bands of materials.
− Dopants : The properties of pure semiconductor crystals can be significantly changed by inserting small quantities of elements from Group III (boron or gallium) or Group V (e.g., arsenic or phosphorous) of the periodic table into the crystal lattice of the semiconductor. These elements, known as dopants, can be diffused or implanted into semiconductors. The properties of the chip (i.e., a thin crystal of silicon) changes when different amounts and different types of dopants are added to semiconductors.
− n-type silicon: When the materials from Group V is added to the crystal lattice, one of the five valence electrons in each dopant atom remains freer to move around. In this case, the dopant is called a donor element because it enhances the electron conductivity of the semiconductor. The resulting semiconductor is called n-type silicon due to the electrons available in the crystal lattice as charge carrier.
− p-type silicon: When the materials from Group III is added to the crystal lattice, holes form due to missing electrons in the lattice. In this case, the dopant is called an acceptor. The resulting seminconductor is called p-type silicon due to the holes become effectively the positive charge carriers.
− Summary: The purpose of doping a semiconductor such as silicon is to elevate and control the number of charge carriers in the semiconductor. In a n-type semiconductor, the charge carriers are electrons, and in a p-type semiconductor, the charge carriers are holes. The interaction between n-type and p-type semiconductor materials (i.e., pn junction ) is the basis for most semiconductor electronic devices.
