










































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
PartI–Linear Quadratic(LQ) optimal control•Continuous-time regulator design•Tuning•Trackingand Non-zerosetpoints•Integral action in LQ control•Certainty Equivalent(CE) control•Guidance Part II–Thruster allocation•General description of thruster allocation•Optimal allocation•SingularitiesPart III–Constrained control•Motivation and classification•Different approaches and examples•Anti-windup
Typology: Lecture notes
Uploaded on 02/06/2012
1 / 53

This page cannot be seen from the preview
Don't miss anything!














































Lecture 7, Spring 2007
TMR4240 Marine Control Systems Department of Marine Technology,
Norwegian University of Science and Technology,
23 Feb 2007
Continuous-time regulator design
-^
Tuning
-^
Tracking and Non-zero set points
-^
Integral action in LQ control
-^
Certainty Equivalent (CE) control
-^
Guidance
Part II–Thruster allocation •^
General description of thruster allocation
-^
Optimal allocation
-^
Singularities
Part III–Constrained control •^
Motivation and classification
-^
Different approaches and examples
-^
Anti-windup
Part IV–Midterm hints
problems:
Regulation: Suppose that the plant output or its derivatives are initially
non-zero. Then, the regulation problem consists of designing thecontrol action that bring the plant output and its derivatives to zero,i.e., bring the plant to zero state. DP is a particular example of this,where the plant is perturbed from its zero conditions by disturbances.
Tracking: The plant output and/or its derivatives are required to follow
some prescribed functions. The tracking problem then consists ofdesigning the controller that achieves this. Trajectory tracking is oneexample of this.
u
OPT
(t)
(control law), over
the time interval [
t^0
,t
f^
] such that
) ), (
), ( (
min
arg
) (^
] , [ ), (^
0
t t u t x V t u
tf t t t u
OPT
∈
=
Subject to
0
0
-^
The functional
V
(i.e. function of a function), measures the deviations from
the desired performenace, and therefore it should be minimised.
-^
Depending on the definition of the cost, this can be posed as a regulator or atracking problem.
-^
The word
``
Optimal´´
here should only be interpreted with respect to the the
particular cost defined—the performance of an optimal controller can be farfrom satisfactory if the cost does not capture the characteristics of thephysical problem!
Lecture 7.1 - TMR4240 Spring 2007
The non-zero set point LQR provides a fist step towards tracking, because
once we are getting close to a set point, we can change to a new set-point.
In this case, we only give the controller the new set point, and the
trajectories followed by the state of the system depend on the tuning ofthe regulator, i.e. it is not a true tracking because we do not follow aspecifies trajectory.
Sp2:
y
d
The actualtrajectory dependon the tuning ofthe LQR
Sp1:
y
d
Sp3:
y
d
x
2
In this example, which state has aheavier penalty inthe
Q
matrix?
x
1
This approach to tracking may be acceptable depending on the particular application.
Sp2:
y
d
The actual trajectory
Sp1:
y
d
x
2
x
1
Desired trajectory
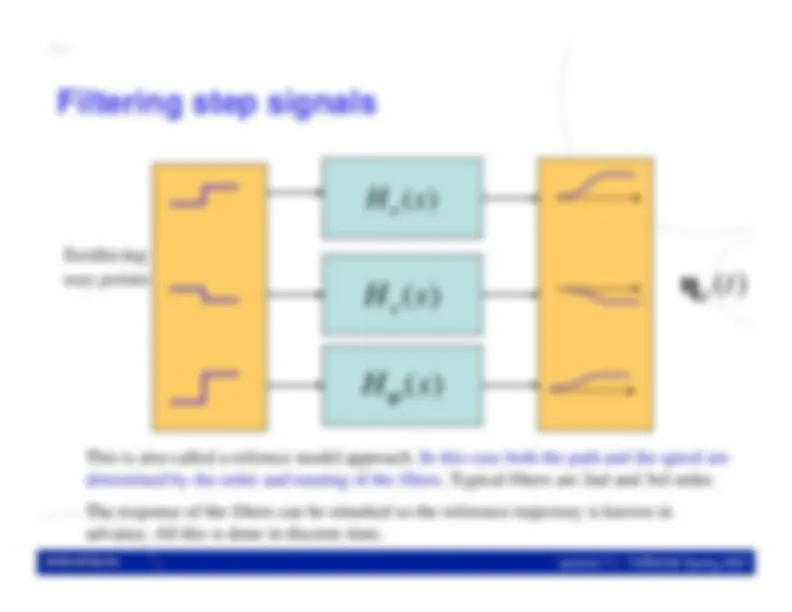
-^
We not only specify the set point, but also the trajectory the system hasto follow on the way
-^
In most problems this trajectory is known is advance.
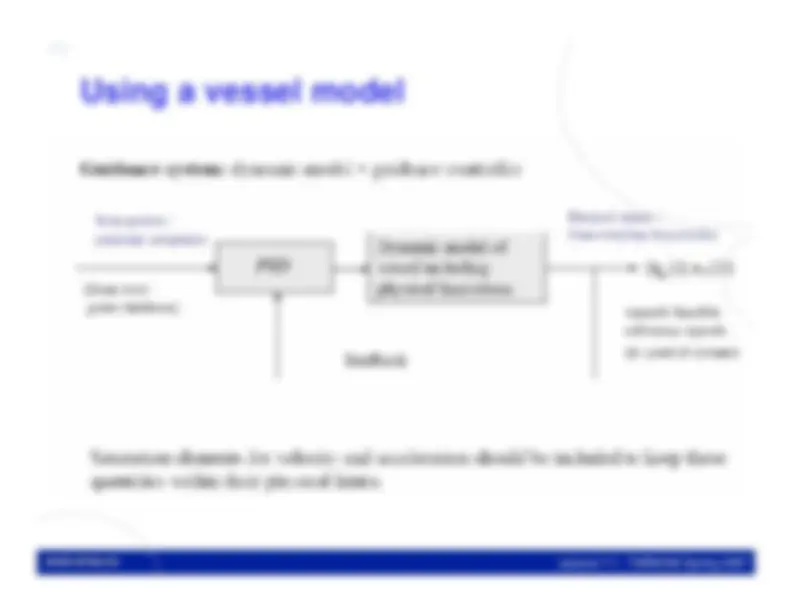
we can augment the system with the states of the autonomous model and theplant or controlled system and design a LQR for the augmented model andpenalize the deviations of the states of the original system from the states ofthe autonomous system.
Reference system
Augmented systemControlled system
Lecture 7.1 - TMR4240 Spring 2007
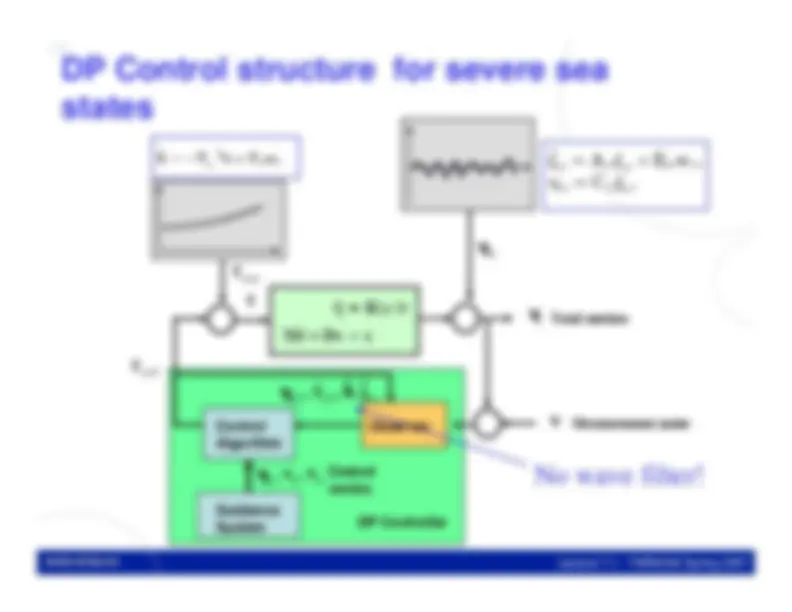
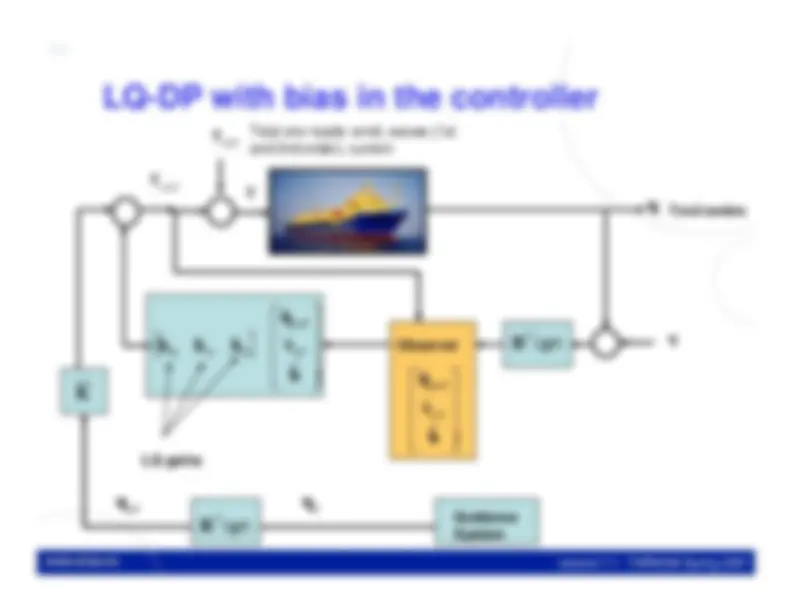
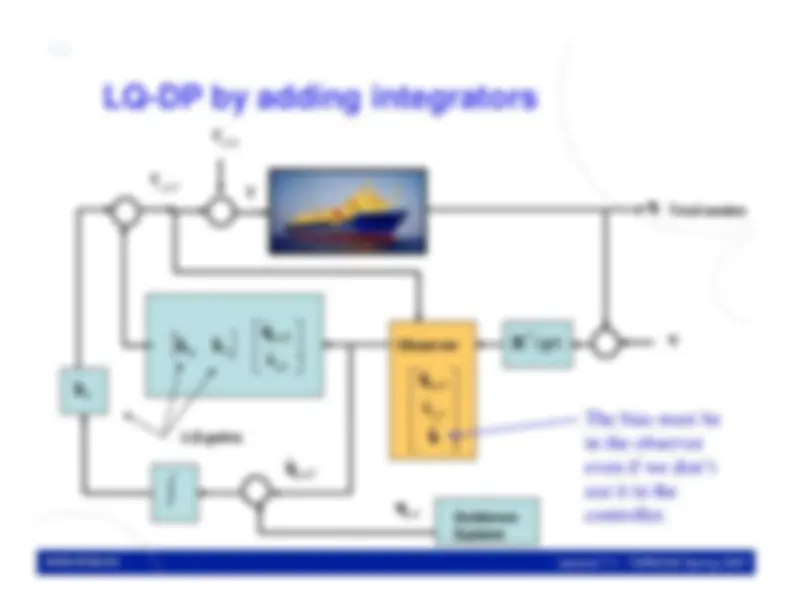
LQ control does not guarantee integral action
per sé
, in
general. Therefore, offsets and constant disturbances may not berejected in steady state. Integral action needs to be enforced in the controller design.